Markov Decision Processes

[Markov Processes]

Introduction to MDPs

Markov Decision Processes는 대부분 RL에서 environment를 의미한다. 환경이 완벽하게 observable한 것을 의미한다. 예를들어 현재 state가 process를 완전히 표현할 수 있다. 거의 모든 강화학습은 MDP 형태로 만들 수 있다.

Markov Property

state는 history에 관련된 모든 정보를 포함하고 있다. 그래서 히스토리는 버려도 된다.

State Transition Matrix

State trainsition probability

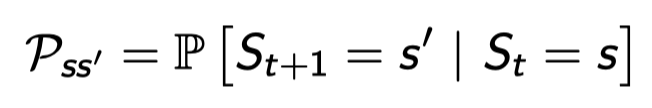t 시간에 s에 있었고 t+1에 갈 수 있는 스테이들에 대한 확률을 나타낸 것.

State transition matrix

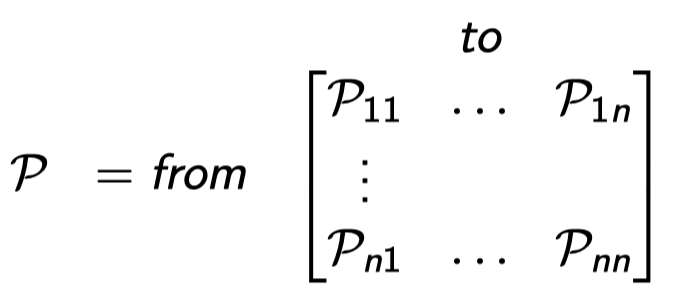
그 확률들을 매트릭스로 나타낸 것. 스테이트는 총 n개가 있고 확률이 0인 칸도 있을 것이다. 그리고 각 row의 합은 1이 된다.

Markov Process

마르코프 프로세스는 memoryless random process이다. 여기서 memoryless의 의미는 어디서 어떻게 왔든 상관없이 미래는 현재에서 결정한다는 뜻(Markov property)이고 random process는 sampling을 할 수 있다는 의미이다. 즉, 마르코프 property를 가진 랜덤 스테이트들의 순서를 의미한다.

즉 마르코프 프로세스를 설명하기 위해서는 S와 P만 있으면 된다.

• S : state들의 집합.
• P : 다음 state로 전이할 확률.

Example : Student Markov Chain Episodes

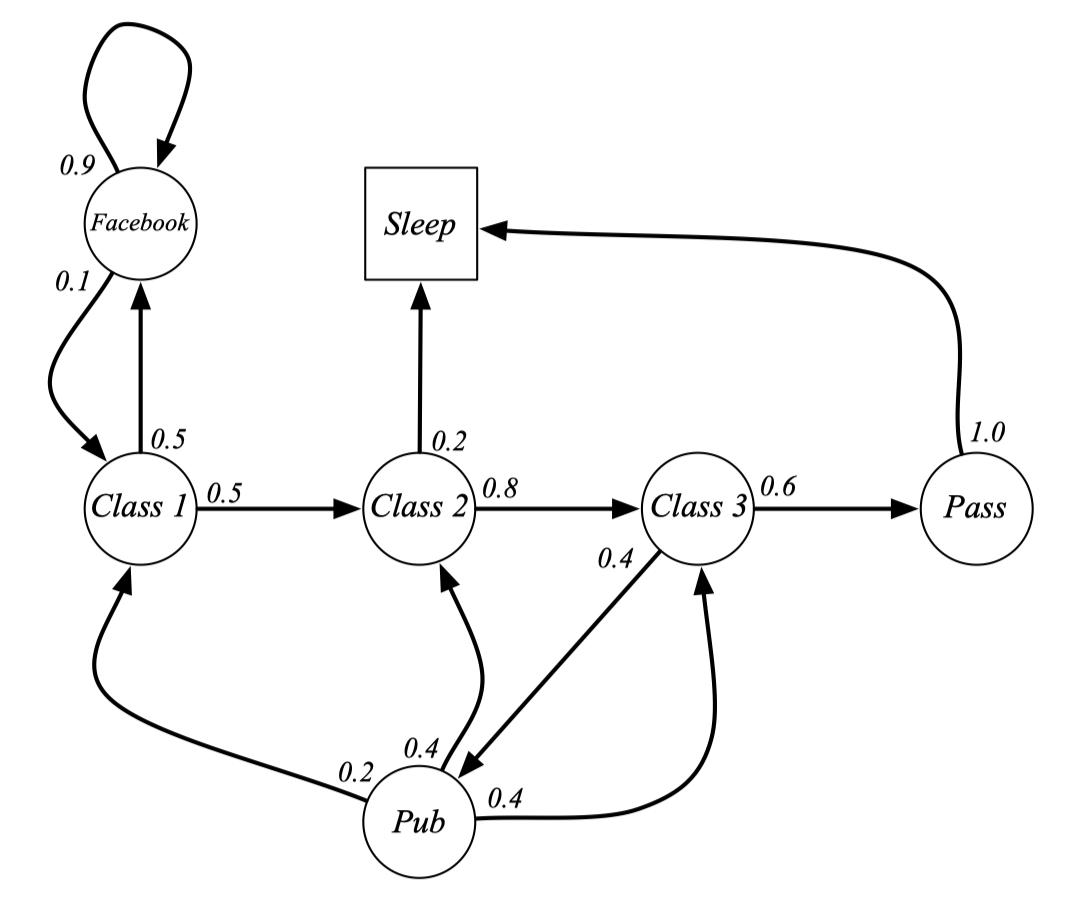
여기서 episode는 한 스테이트에서 시작해서 final(terminate) state까지 가는 걸 의미한다. 마르코프 체인의 시작 스테이트가 C1인 상태에서 에피소드를 샘플링을 해보자.

• C1 C2 C3 Pass Sleep
• C1 FB FB C1 C2 Sleep
• C1 C2 C3 Pub C2 C3 Pass Sleep

여기서 transition matrix를 만들어본다. Transition matrix는 스테이트들의 집합과 트랜지션들의 집합으로 표현이 가능하다고 했으니 스테이트들은 이미 알고 있어서 매트릭스를 그릴 수 있다. (빈 칸은 0)

[Markov Reward Process]

Markov Reward Process

마르코프 프로세스 설명에는 S, P만 필요했지만 마르코프 리워드 프로세스에서는 S, P, R, \(\gamma\)도 필요하다. 이 4개로 마르코프 리워드 프로세스를 완전히 표현가능하다.

• S : 스테이트들의 집합
• P : 트랜지션 확률 매트릭스
• R : 리워드 함수 (어떤 스테이트에 도착하면 어떤 리워드를 줘라.를 스테이트 별로 정의 해두는 것.)
• \(\gamma\) : discount factor

Example : Student MRP

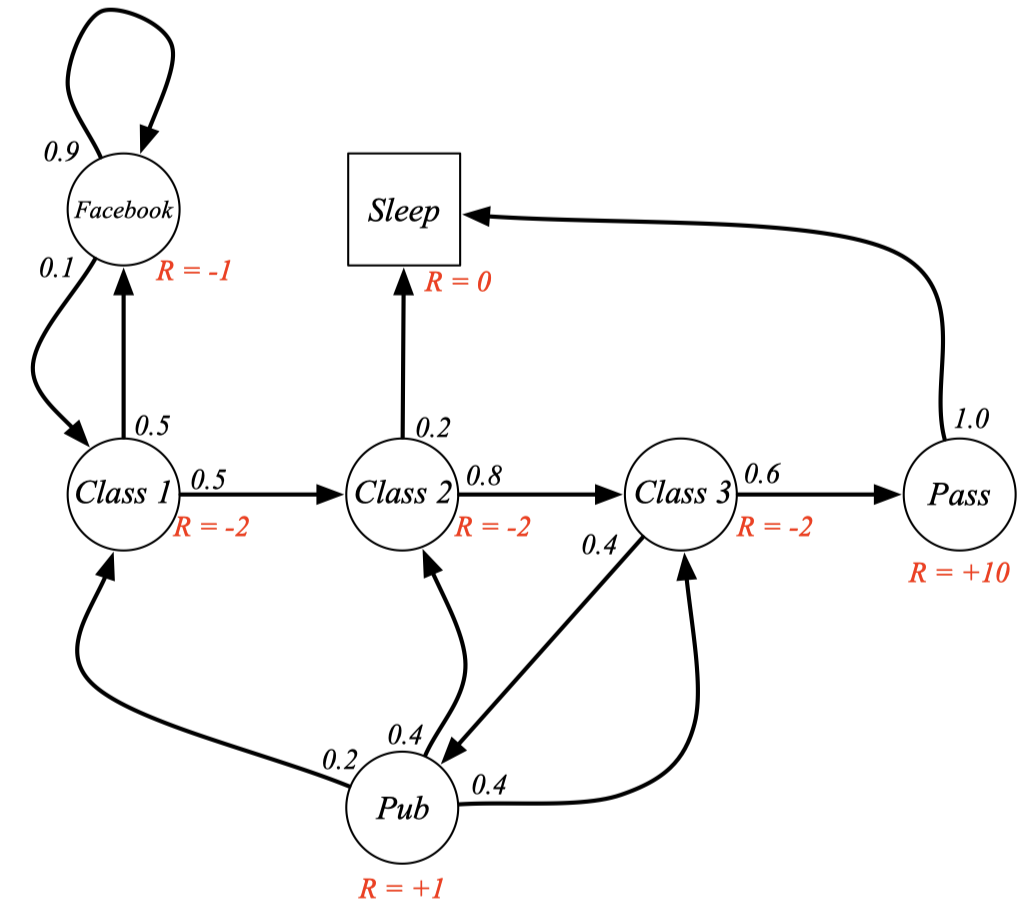
빨간색 글씨로 리워드가 추가된 것을 볼 수 있다.

Return

“강화학습은 return을 최대화 하는 것이다!!”. 흔히 말해서 reward를 최대화 하는게 아닌가?? 라고 생각을 하는데 여기서 return과 reward는 다른 개념이다. 사실 return 이 더 정확한 표현이라고 할 수 있다. return은 약간 감마를 통해서 total discounted reward를 계산해내는 것이다.

강화학습의 목표는 culmulated total discounted reward를 maximize하는 것 :)

• 감마가 0에 가까우면 단기적으로 evaluation 하게 됨.
• 감마가 1에 가까우면 장기적으로 evaluation 하게 됨.

대부분의 Markov reward와 decision process들은 discount를 사용한다. 근데 왜 감마를 통해서 discount 해야 하지?라는 의문이 들 수 있다.

• 수학적으로 편리하다. 이 discount 덕분에 수렴성이 증명이 된다.
• 만약 모든 에피소드들이 terminate로 끝나는게 보장이 되면 감마를 1로 해도 될 수도 있다고 함.

Value Function

return의 기댓값. 어떤 스테이트에 왔을 때 계속 샘플링하면서 에피소드를 만들어 감. 그럴 때 에피소드마다 리턴이 생기게 됨.

Example: Student MRP Returns

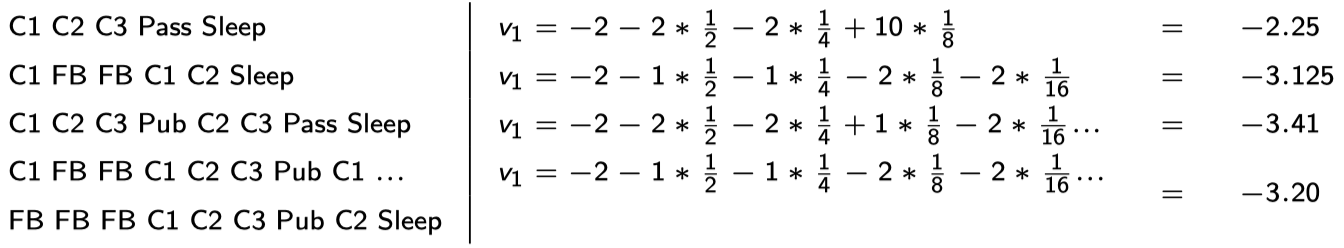
같은 C1에서 시작을 해도 어떻게 샘플링을 하느냐에 따라 discount된 return 값이 달라진다. 이것을 평균 내서 구하게 되면 나중에 C1에 도착했을 때 얻을 수 있는 reward를 대충 예상할 수 있게 된다.

Example: State-Value Function for Student MRP (1)

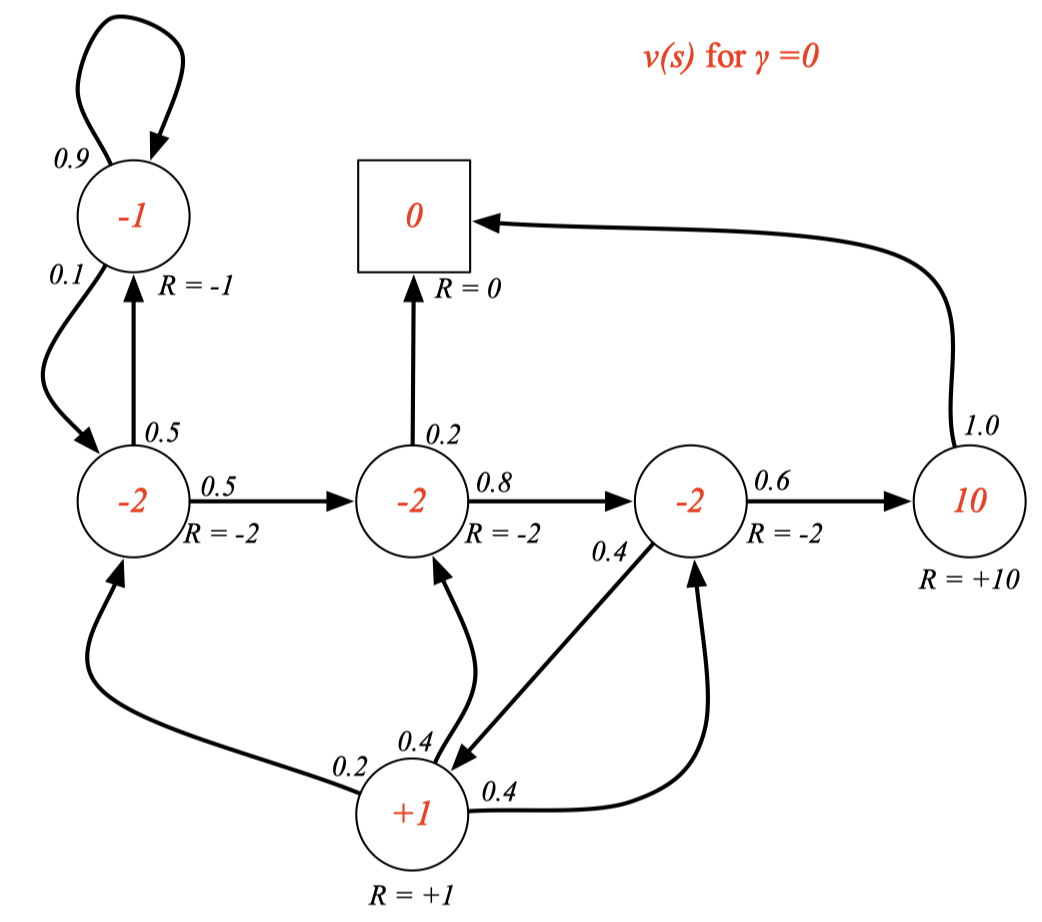
discount가 없을 때 state-value function을 각 state마다 빨간색으로 구해 놓은 것이다. 감마가 0이기 때문에 discount가 없고 리워드랑 값이 똑같다 (그 순간의 값만 받고 그 이후의 값은 다 무시)

Example: State-Value Function for Student MRP (2)

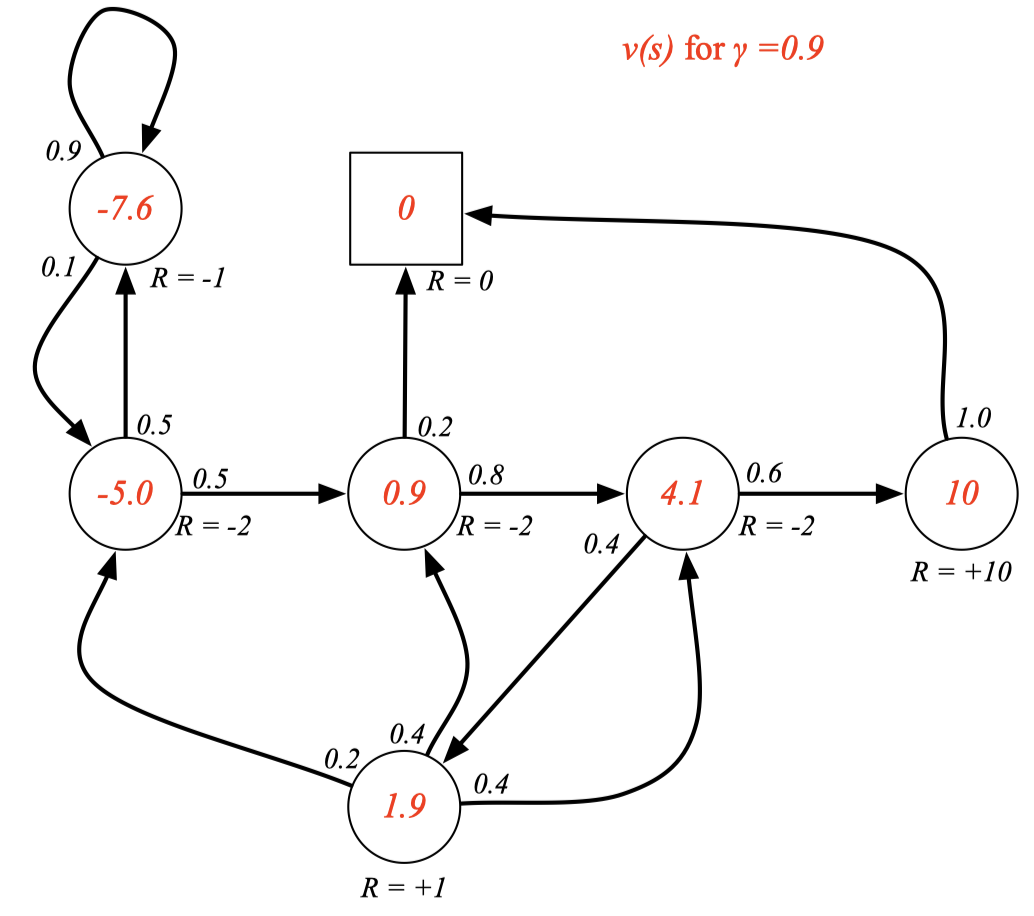
Example: State-Value Function for Student MRP (3)

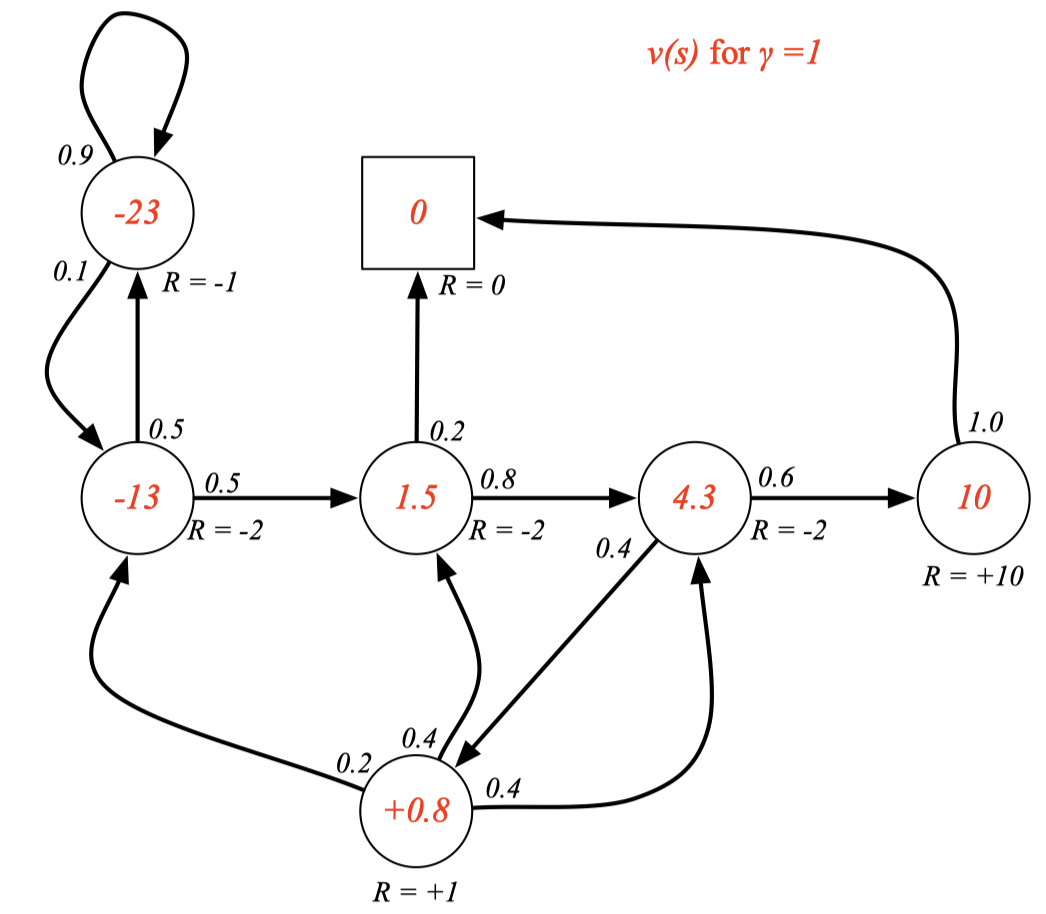
Bellman Equation for MRPs

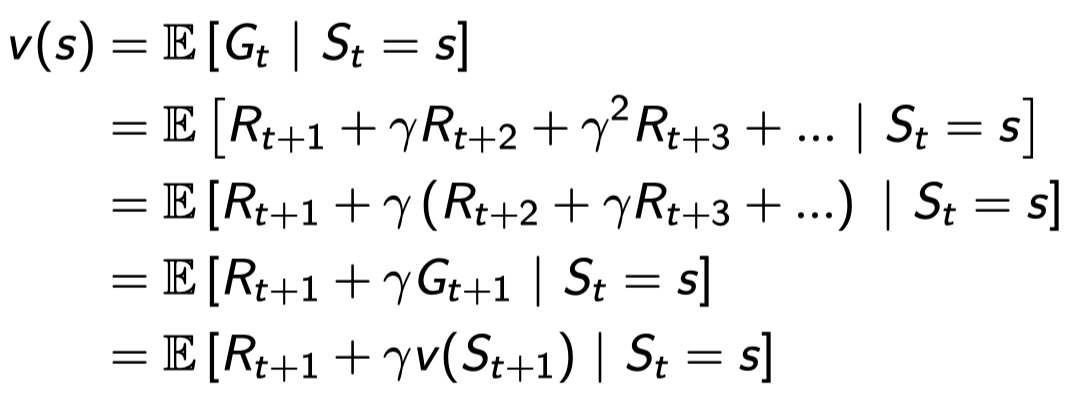
• 즉각적인 reward \(R_{t+1}\)
• 다음 스테이트에서의 discounted value \(\gamma v(S_{t+1})\)

Expectation 안에 Expectation이 들어 갈 수 있어서 \(G_{t+1}\)의 기댓값인 \(v(S_{t+1})\)로 바뀔 수 있다. 현재 스테이트 s에 있을 때 value는 한 스텝을 가서 얻는 \(R_{t+1}\) 더하기 다음 스테이트에서 얻는 value에 \(\gamma\)를 곱한 것과 같다. 즉, 한 스텝을 더 가서 보는 것이다.

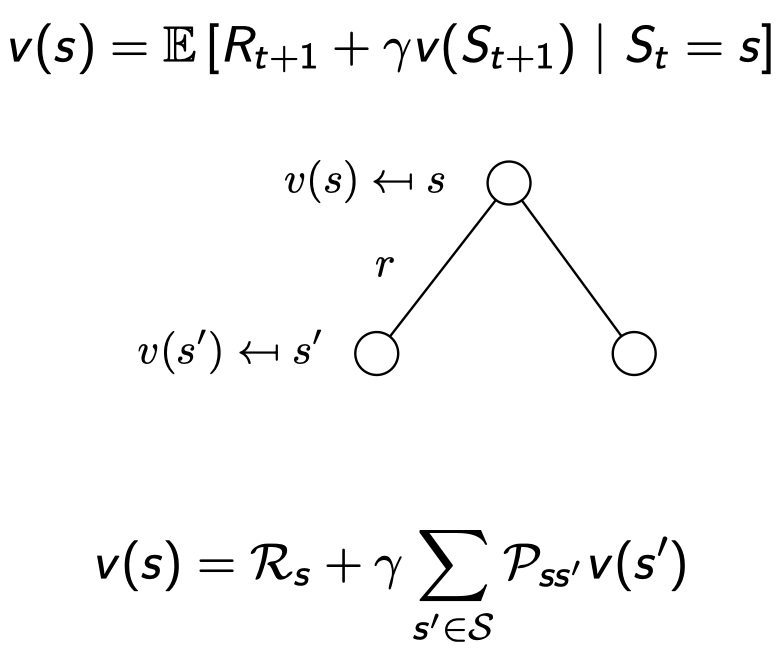
즉, 갈 수 있는 모든 스테이트들에 대해 확률을 곱해서 더하고 현재 스테이트에서 얻을 수 있는 return 값을 더한 것이다.

Bellman Equation in Matrix Form

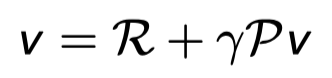
위의 Bellman Equation은 벡터와 매트릭스 형태로 다시 표현 될 수 있다.

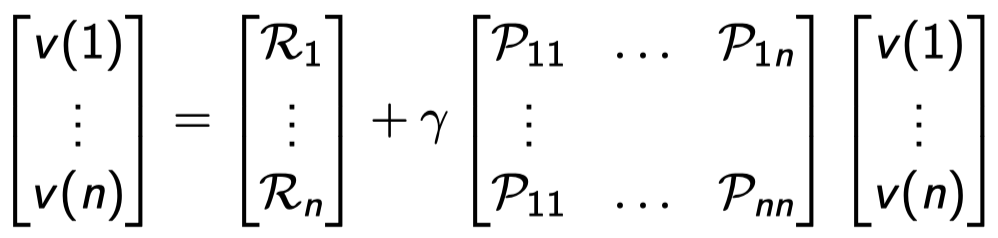
Solving the Bellman Equation

Bellman equation은 linear equation이고 directly하게 풀 수 있다.

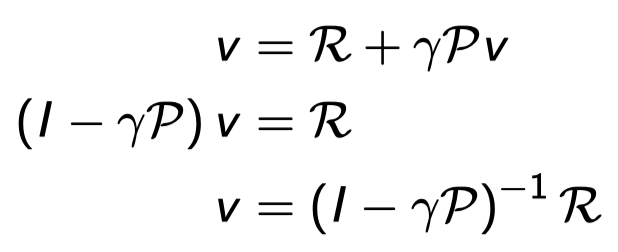
이전의 식을 정리하면 위와 같아지는데 여기서 R, P, \(\gamma\)는 MRP의 정의에 다 주어져있는 정보다. 고로 그냥 대입해서 풀어주기만 하면 바로 value function을 구할 수 있다.

시간 복잡도는 n개의 state에 대해 \(O(n^3)\)인데 생각보다 계산이 코스트가 있기 때문에 작은 MRPs에 대해서만 direct solution이 가능하다. 큰 MRPs에 대해서는 조금조금씩 iterative 한 방식으로 풀어나가야 한다.

• Dynamic programming
• Monte-Carlo evaluation
• Temporal-Difference learning

[Markov Decision Processes]

Markov Decision Process (MDP)

MDP는 MRP에 decision (=action)이 더 붙은 것이다. 모든 스테이트들이 Markov한 environment다.

• A는 action들의 finite set이다.

Example: Student MDP

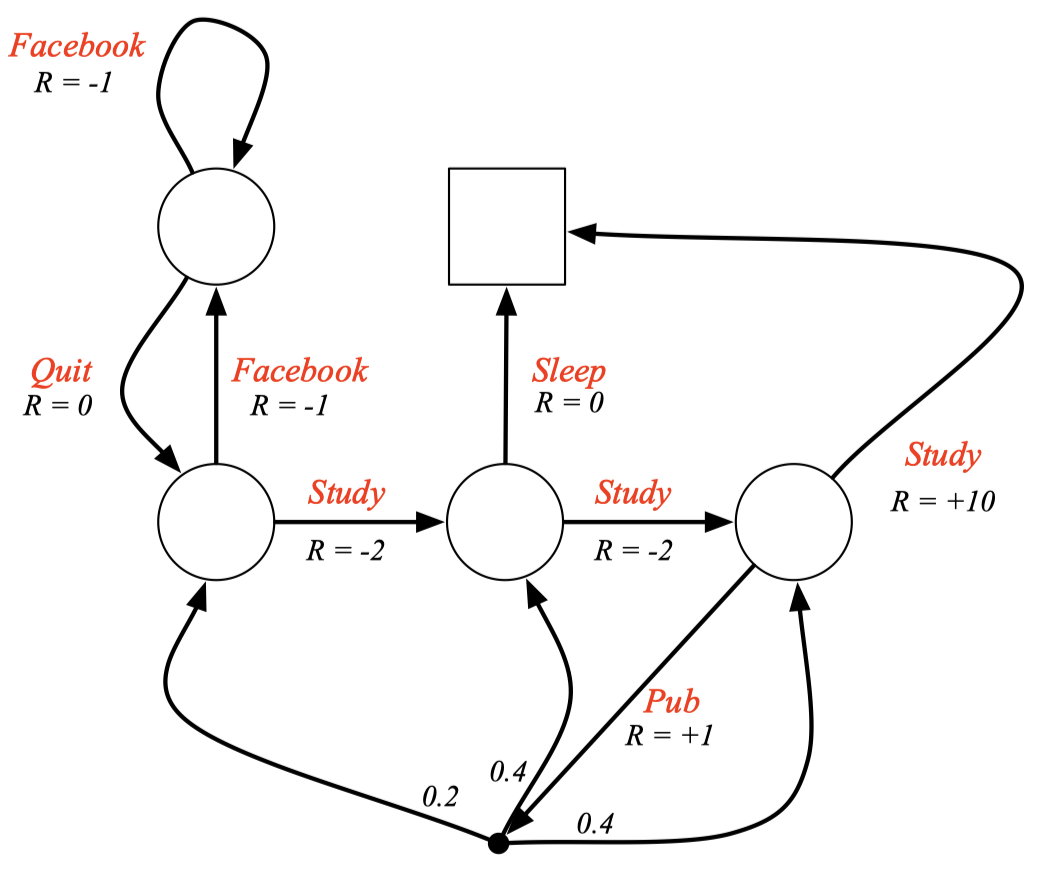
1. State들의 이름이 사라졌음.
2. Action마다 이름이 생기고 reward를 받음. (MRP에서는 state마다 reward 받았었음.)

아래 Pub 부분을 보면 Action을 행하면 무조건 어느 스테이트로 가는게 아니라 확률적으로 state로 가게 됨. 즉, Pub 행동을 하면 0.2, 0.4, 0.4의 확률로 다른 스테이트로 가게 되어 있음. 다른 Study같은 경우도 확률이 없는게 아니라 1의 확률로 다음 스테이트를 가고 있는 중이고 그림에는 검은 점과 1.0이 생략되어있다고 보면 된다.

Policies (1)

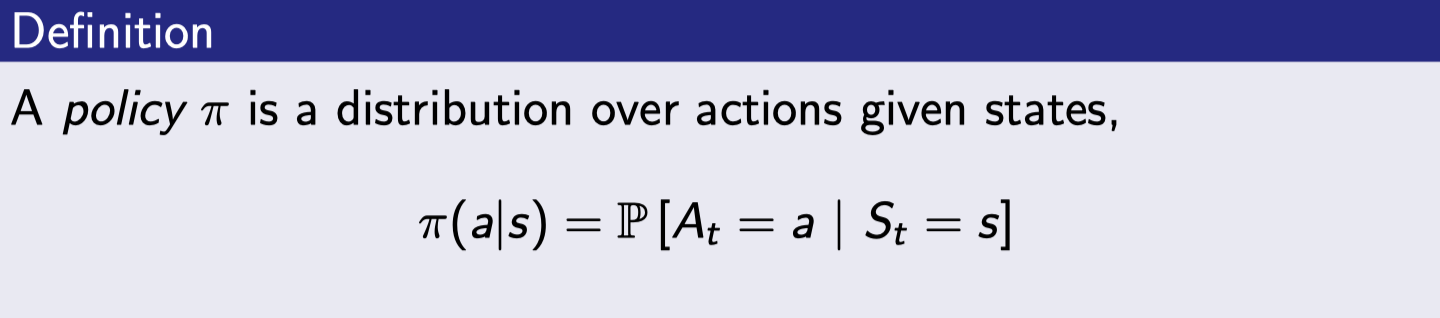
Policy는 주어진 스테이트에서 할 수 있는 action들의 확률분포이다. Agent의 행동을 완전히 정해주며 MDP policy들은 history가 아닌 현재 스테이트에 의존한다.

여기서 MDP 는 environment의 것을 나타내면 policy는 Agent의 것이라 그림에 따로 표현되지는 않는다.

Policies (2)

(이 장은 그냥 이런게 있구나~ 하고 넘어가도 됨.)

MDP \(M = <S,A,P,R,𝛾>\)와 policy \(π\)가 주어져있을 때, (=MDP 정해져있고 policy 고정인 상태)

• 스테이트들의 sequence \(S_1, S_2,\) …는 Markov process \(<S, P^π>\)이다.
• 스테이트와 reward sequence \(S_1, R_2, S_2,\) …는 Markov reward process \(<S, P^π, R^π, 𝛾>\)이다.

where,

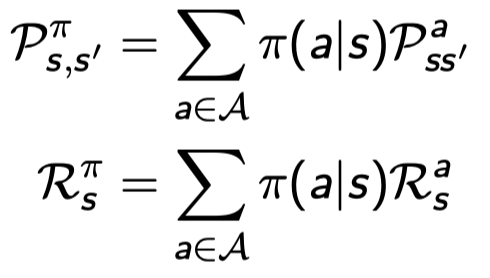
즉, MDP를 위의 식들을 이용해서 MP 또는 MRP로 바꿀 수 있다.

위에서 \(P_{ss'}^a\)는 s에서 a를 했을 때 s’로 갈 확률인데. 이전의 그냥 \(P_{ss'}\)는 m×m 행렬이었다면 얘는 a의 조건이 추가되면서 엄청나게 큰 matrix가 된다.

Value Function

value function은 2 가지로 나뉜다.

state-value function

input은 state 하나이다. action이 따로 없었던 MRP와는 달리 action이 추가되면서 policy π가 추가됐다. 여전히 그 의미는 현재 스테이트 s에서 출발했을 때 얻을 수 있는 return의 기댓값을 의미한다.

action-value function

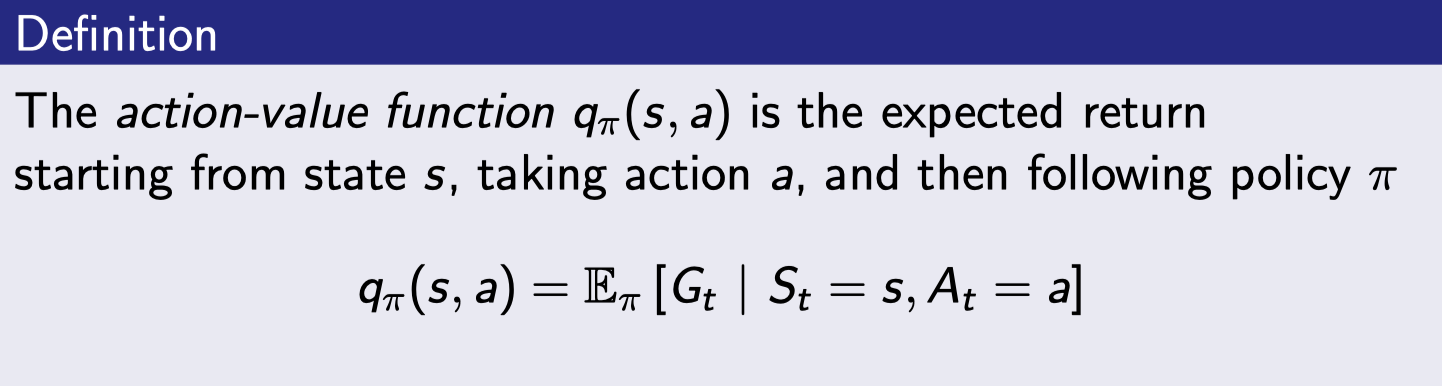
다른 말로 state action-value function이라고도 부르며 Q함수라고도 부른다. (Deep Q learning 할 때 그 Q 함수이며 얘를 학습시키는게 Deep Q learning이다). input은 state와 action 2개가 들어간다. state s에서 action a를 했을 때 그 이후에는 policy π를 따라서 게임을 끝까지 진행했을 때 return의 기댓값을 의미한다.

Example: State-Value Function for Student MDP

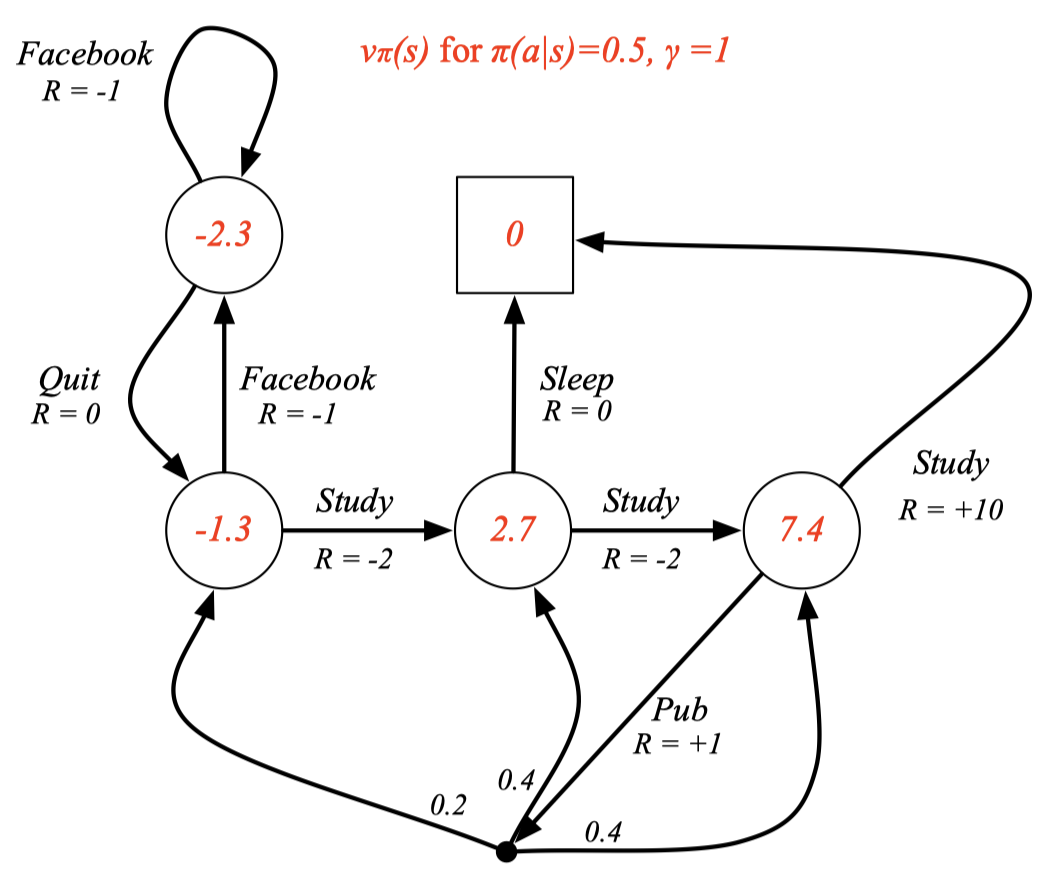
\(π(a \vert s) = 0.5\) 의 의미는 모든 state에서 각각의 action들의 확률이 다 0.5 인 policy를 의미한다. 아직 빨간 숫자들을 구하는 방법은 모른다.

Bellman Expectation Equation

이제 두 value function들을 Bellman equation으로 나타내보자.

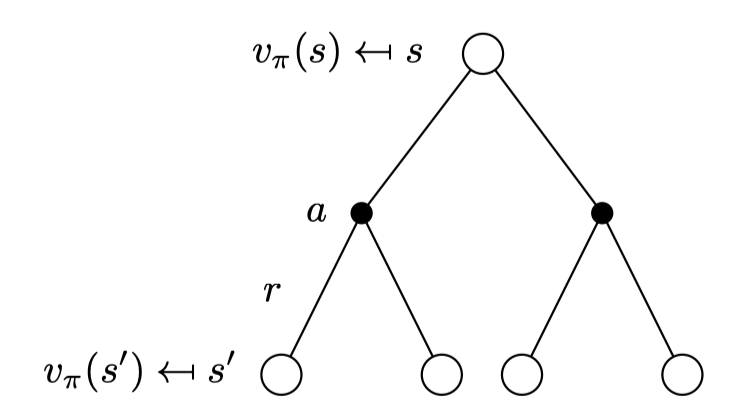
state-value function은 아래와 같이 decompose 될 수 있다: 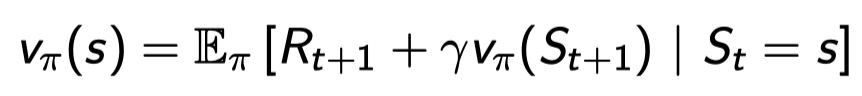일단은 한 스텝을 가고 그 다음 스테이트부터 π를 따라서 가는 것과 같다.

action-value function은 아래와 같이 decompose 될 수 있다:

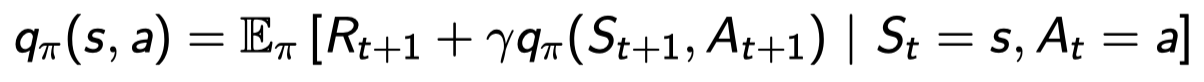스테이트 s에서 action a를 해서 일단 \(R_{t+1}\)를 받고 다음 state에서 다음 액션을 하는 것의 기대값들. 여기서 다음 액션은 π에 의해 정해짐.

Bellman Expectation Equation for \(V^π\)

v를 q 함수로 나타내보자.

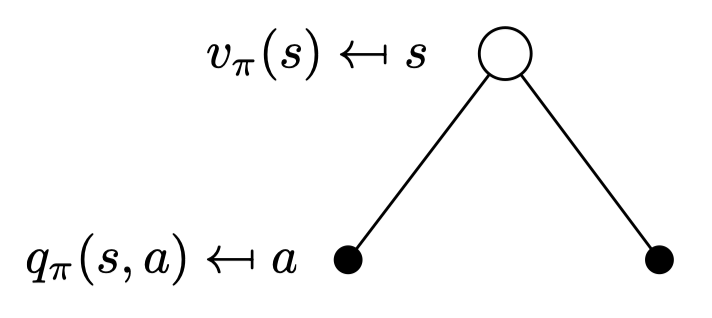
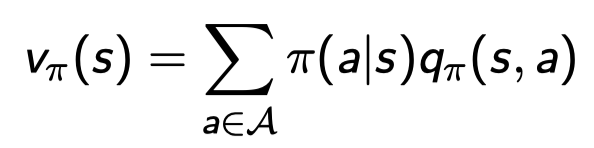
policy에 따라 s에서 a할 확률 × s에서 a를 했을 때 받는 R 들의 합이다. 이 식에는 𝛾가 곱해져있지 않은데 이는 어디에 도착하는게 아니라 그냥 행동하면..이라는 확률을 의미하기 때문에 없다.

Bellman Expectation Equation for \(Q^π\)

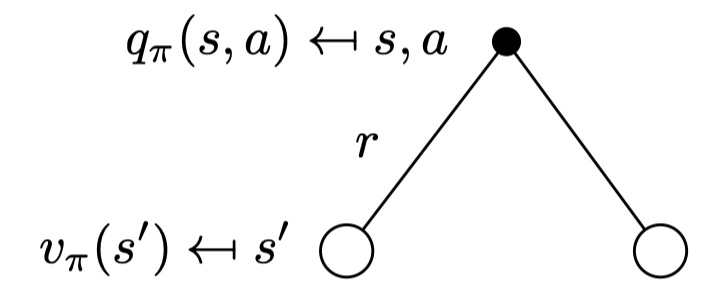
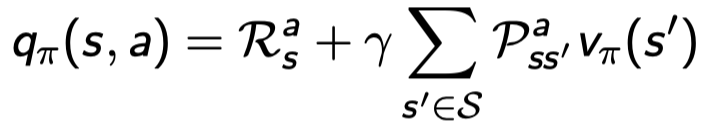
q 역시 v 로 표현이 가능하다.

일단 s에서 action a를 했으니까 \(R_s^a\)를 받는다. 그리고 다음 스테이트인 s’에서 받을 수 있는 value를 계산하는데 이 때 s에서 a를 하면 정확히 어느 state로 떨어질지 모르니까 확률 \(P_{ss'}^a\)와 해당 s’ 스테이트에서 얻는 value function인 \(v_π(s')\)를 서로 곱해준다. 여기서 도착의 의미가 있으니까 discount 𝛾도 곱해준다.

s에서 a 행동을 하고 그 뒤로는 π를 따랐을 때 얻을 return 의 기대값이다.

Bellman Expectation Equation for \(V^π (2)\)

앞서 봤던 두 식을 결합한다. v 식안의 q 함수를 바로 위에서 정의했던 q함수로 대입을 한다.

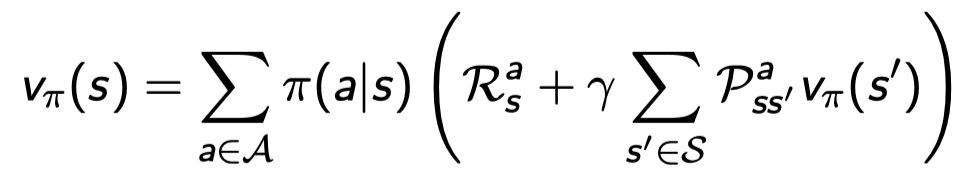
이렇게 되면 두 개의 그림을 연결시킨 2 step으로 볼 수 있다.

Bellman Expectation Equation for \(Q^π (2)\)

마찬가지로 기존 q 함수 안에 v식을 대입할 수도 있다.

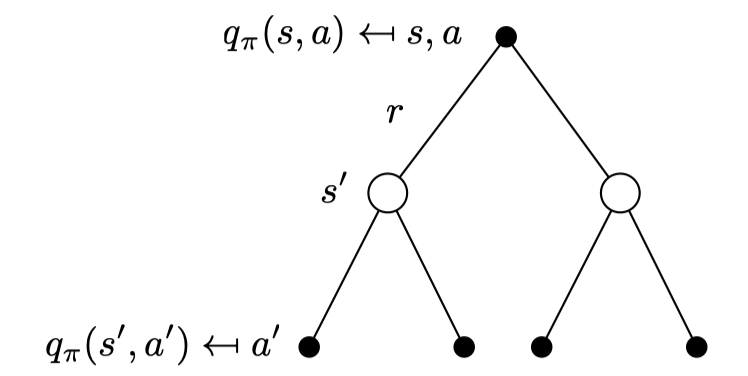
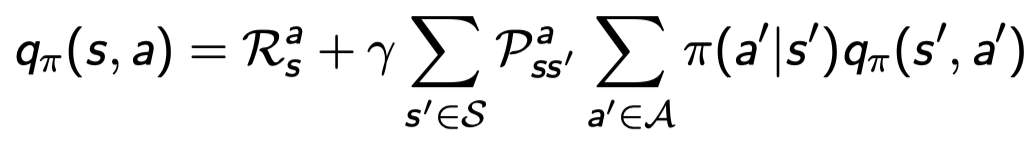
Example: Bellman Expectation Equation in Student MDP

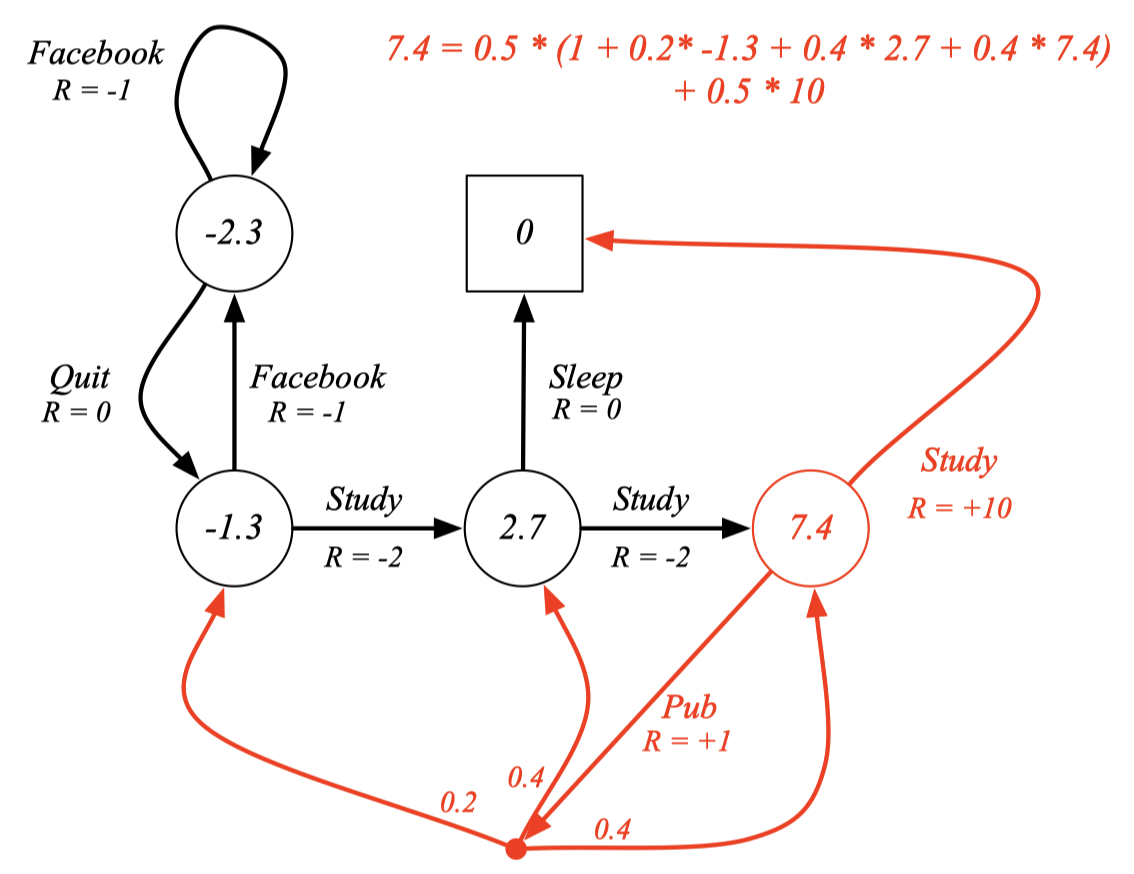
제일 오른쪽 스테이트의 value 7.4가 어떻게 계산되었는지 보자. 일단 policy에 따라 어떠한 액션이든 그 확률은 0.5이다. 이제 액션을 취함으로써 얻을 수 있는 R을 더하고 (Pub의 경우에는 1) 각 스테이트로 갈 확률 × 각 스테이트들의 value function을 곱해주고 다 더한다.

Bellman Expectation Equation (Matrix Form)

Bellman expectation equation은 다시 matrix 형태로 표현이 가능하다.

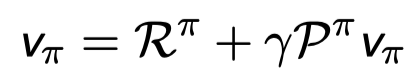
또한 역행렬을 이용하여 direct solution을 바로 구할 수 있다.

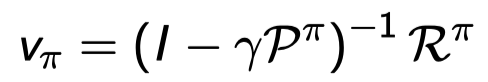
역시나 단점은 MDP가 커지면 풀 수 없다. (계산량 투머치)

Optimal Value Function

Optimal하다의 의미는 최적의 해라는 의미이고 노테이션은 *를 사용한다. 즉, optimal state-value function \(v_*(s)\)는 존재하는 모든 policy π를 따랐을 때 그 중에서 maximum value function을 의미한다. 역시나 optimal action-value function의 경우 모든 policy들 중 maximum action-value function을 의미한다.

Optimal value function은 MDP에서 가장 최상의 성능을 명시하며 이 optimal value function을 알게 되었을 때 MDP는 "풀렸다"라고 말한다.

Example: Optimal Value Function for Student MDP

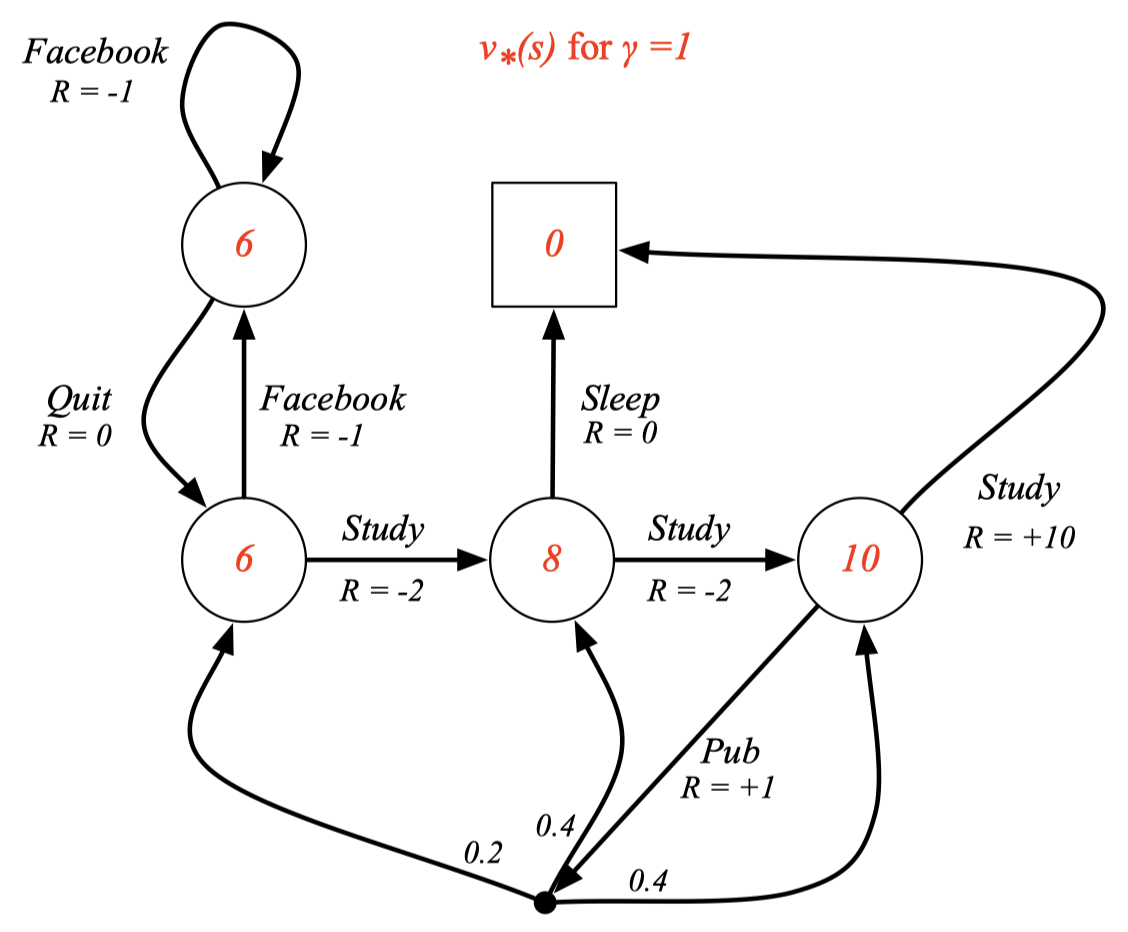
여기서 각 숫자들이 Optimal value function을 의미한다.

Example: Optimal Action-Value Function for Student MDP

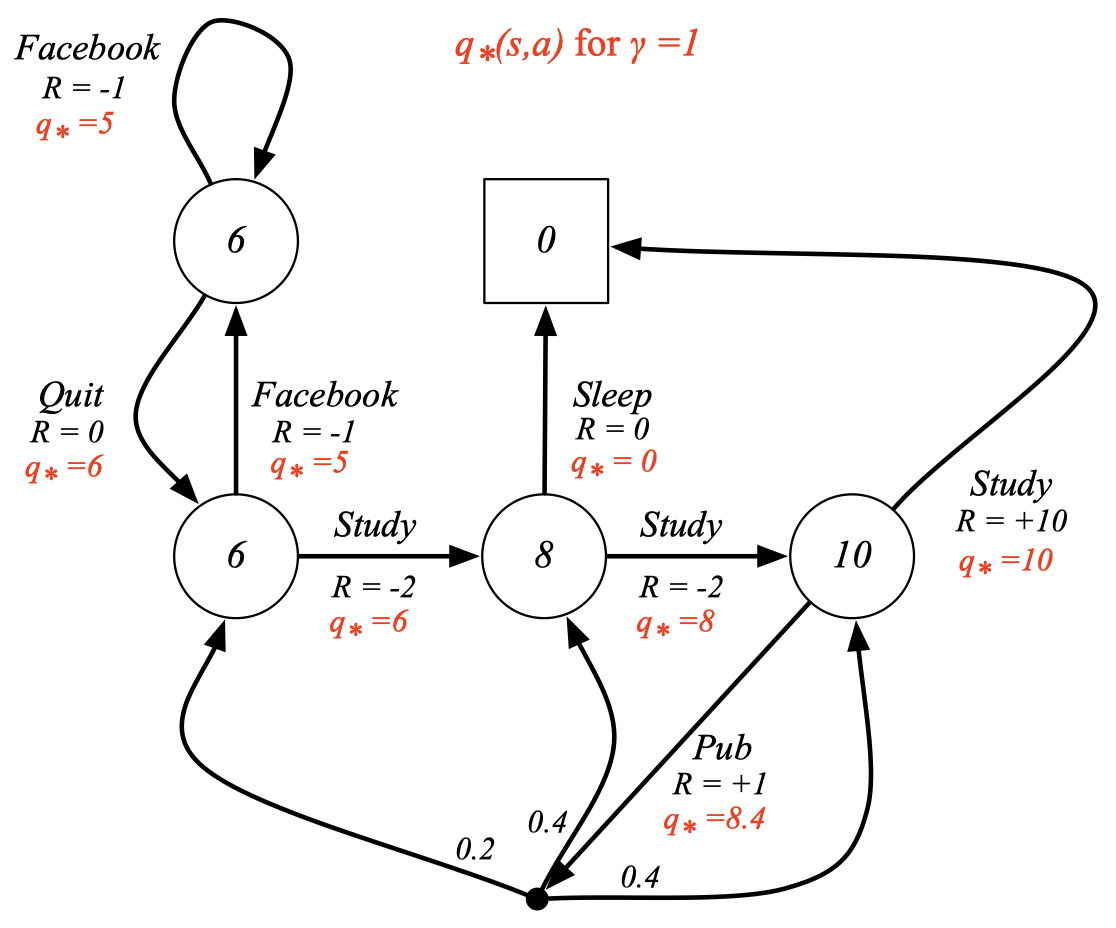
빨간 글자의 \(q_*\)가 optimal action-value function을 의미한다.

Optiaml Policy

둘 중 더 나은 policy를 알아내기 위해 partial ordering을 정의하자.

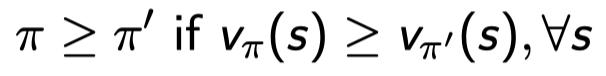
위 식은 항상 비교가 가능한 건 아니지만 비교 가능한 조건이 존재한다. Policy π를 따랐을 때의 모든 state-value이 π’를 따랐을 때의 것보다 좋았을 때 π가 π’와 같거나 더 뛰어나다라고 말할 수 있다. 대신 여기서 하나의 state-value라도 π’의 것보다 더 좋다라고 말할 수 없다.

• 모든 optimal policy들을 따라가면 그 때의 state-value는 optimal value function과 같다.
• 위의 성질은 q에 대해서도 동일하게 성립한다.
• optimal policy가 하나일 필요는 없다. 여러 개일 수도 있어 all을 붙인다.

Finding an Optimal Policy

Optimal policy는 \(q_*(s,a)\)를 최대화함으로써 찾을 수 있다.
즉, \(q_*\)를 아는 순간 optimal policy 하나도 반드시 찾아지게 되어있음.

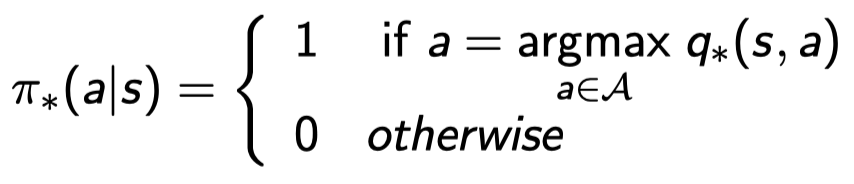
위 식의 의미는 optimal action-value function \(q_x\)의 action을 따라할 확률이 1이고 그 이외의 action에 대한 확률은 0인 policy가 있다고 하자. 그럼 그 policy는 마냥 \(q_*\)를 따라다닐 것이다. 그러므로 당연하게 optimal policy가 된다.

Policy는 본디 각 action에 대한 확률을 말해주기 때문에 stochastic 하지만 모든 MDP는 항상 하나의 deterministic optimal policy를 가지게 된다.

Optimal Policy for Student MDP

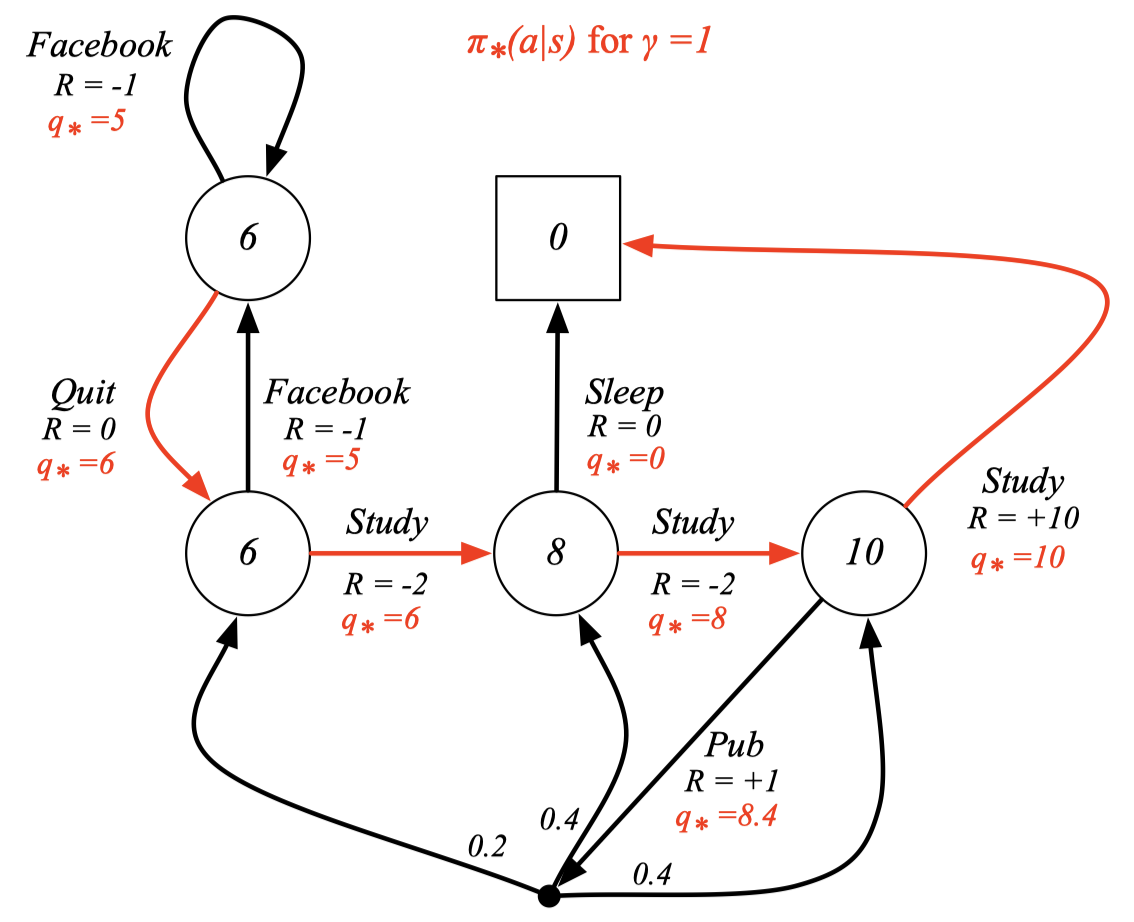
주어진 MDP에서 best \(q_*\)을 따라갔을 때의 경로가 optimal이다. 즉, 빨간 선들이 optimal policy를 의미한다.

Bellman Optimality Equation for \(V_*\)

아까 봤던 식들은 Bellman Expectation Equation이었고 지금은 Bellman Optimality Equation이다. 이는 optimal policy에 Bellman equation을 적용하는 것을 의미한다.

Optimal value function들은 Bellman optimality equation에 재귀적으로 연관된다.

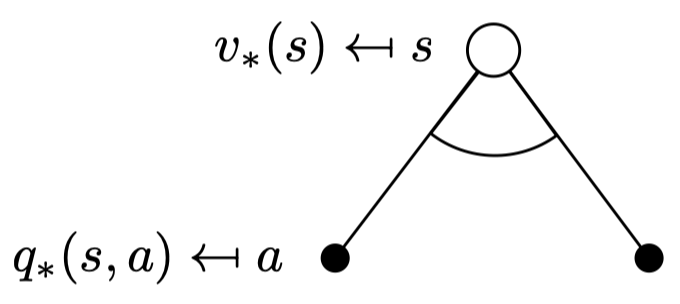
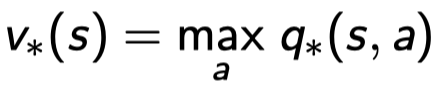
\(q_*\)값들이 action a 마다 존재하는 데 그 값을 maximize하는 (제일 큰) a의 \(q_*(s,a)\)가 \(v_*(s)\)이다. 그냥 스테이트에 달려있는 액션 중에 \(q_*\)값이 젤 큰 애 선택하면 된다.

Bellman Optimality Equation for \(Q_*\)

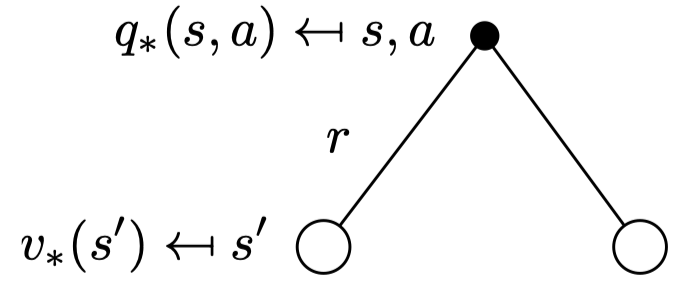
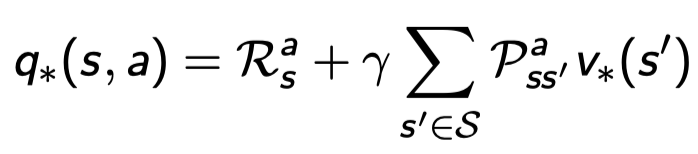
액션을 취하고 다음 state로 갔을 때를 의미하기 때문에 일단 리워드 \(R_s^a\)를 받고 더한다.

Bellman Optimality Equation for \(V_*\) (2)

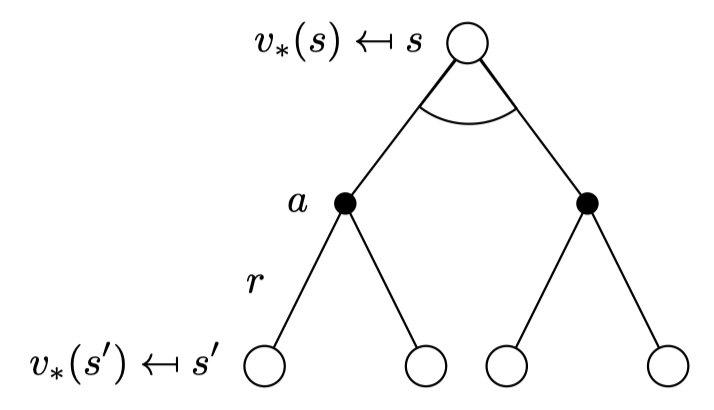
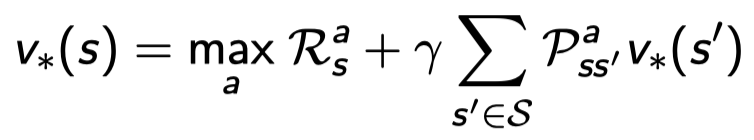
역시나 state-value function에 action-value function을 그대로 대입한다. 그러나 이 식은 Bellman expectation eq와 달리 linear equation이 아니다. 바로 선형적인 식이 아닌 max 함수 때문이다. Max의 존재 때문에 더 이상 선형적이지 않아서 역행렬을 구할 수 없다. 즉, closed form으로 풀 수 없다. 이것이 Bellman Expectation eq와 다른 점이다.

Bellman Optimality Equation for \(Q_*\) (2)

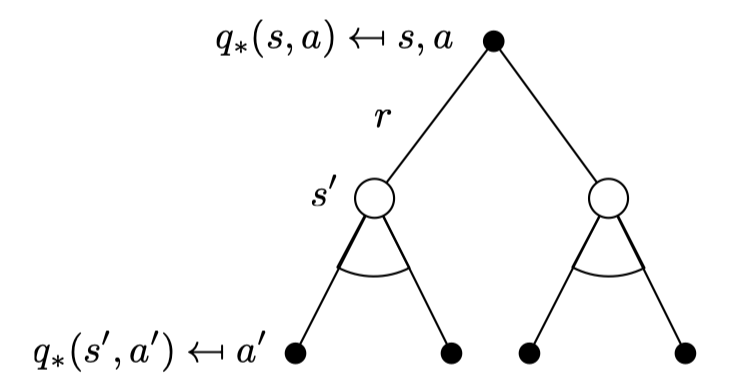
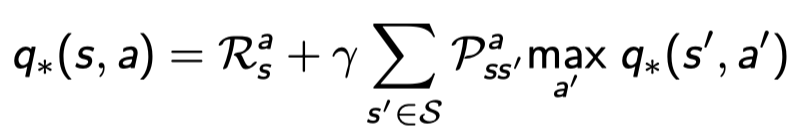
Example: Bellman Optimality Equation in Student MDP

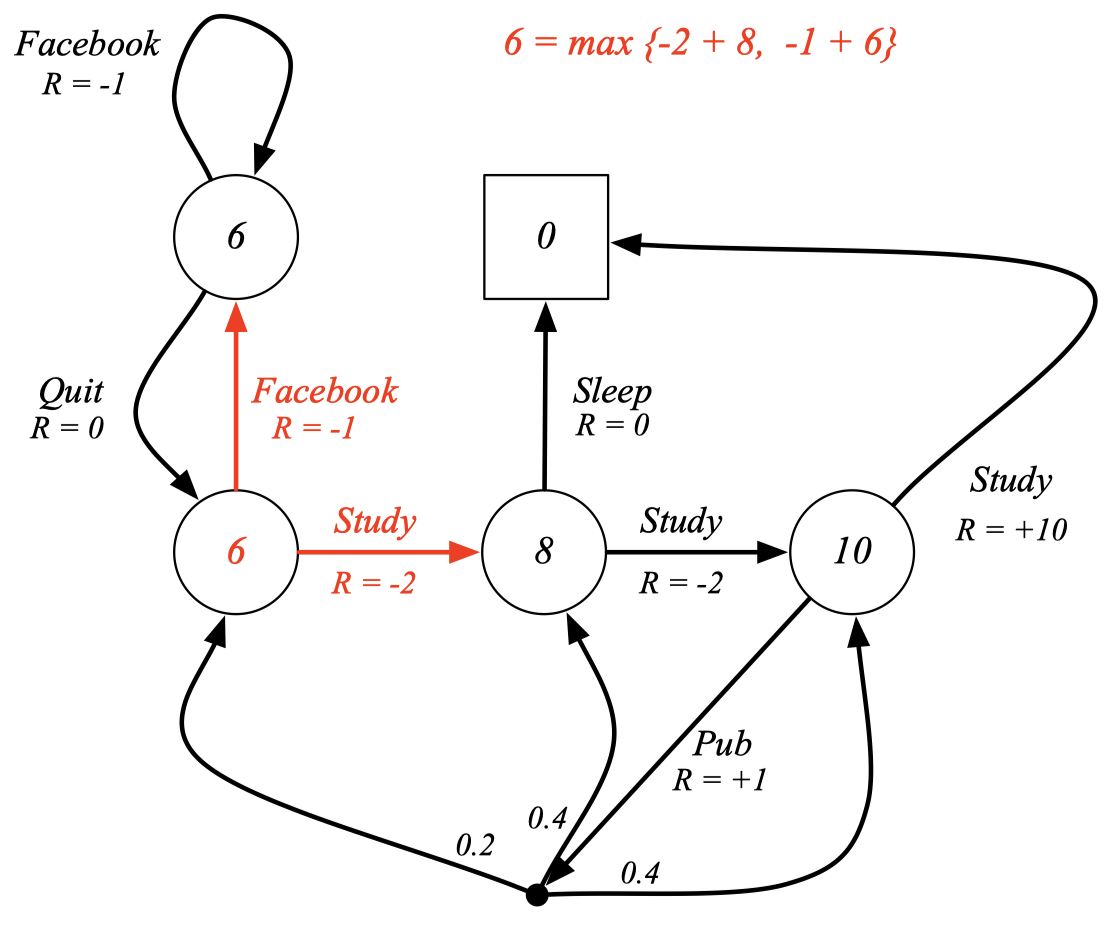
MDP에서도 max를 통해 최적값을 구해내는 것을 볼 수 있다.

Solving the Bellman Optimality Equation

• Bellman Optimality Equation은 non-linear 하다.
• 고로, closed form solution이 없다. (in general)
• 많은 iterative solution methods를 거쳐야 한다.
  • Value iteration
  • Policy iteration
  • Q-learning
  • Sarsa

David Silver 교수님의 강의자료를 참고하였습니다.