Designing Network Design Spaces (RegNet)

Ilija Radosavovic, Raj Prateek Kosaraju, Ross Girshick, Kaiming He, Piotr Dollár
[Facebook AI Research (FAIR)]
[Submitted on 30 Mar 2020]
arXiv:2003.13678

올해 3월에 나온 네트워크 모델 RegNet에 대한 논문이다. 최근까지 최고의 성능을 보여주던 EfficientNet보다 빠르고 성능이 좋은 모델이다.

사실 이런 네트워크가 나온지 몰랐는데 다른 논문에서 해당 모델을 사용하길래 읽어본 논문이다.

EfficientNet처럼 하나의 best model을 만드는 것이 중점이 아니라 뛰어난 모델을 어떤 세팅에서도 사용할 수 있도록 design space를 디자인 하는 것이 논문의 중심이 된다.

요즘 architecture를 만드는 방법으로는 manual한 방식과 neural architecture search (NAS) 방식이 많이 사용되고 있다. Manual은 모델을 직접 만드는 것을 의미하고 NAS는 특정한 search space 안에서 좋은 모델을 자동으로 찾아준다. 자동으로 찾아준다는 장점으로 NAS가 많이 사용되고 있지만 이런 방식은 특정 세팅에만 적잡한 single network instance를 만들기 때문에 general하지 않다는 단점이 존재한다.

그래서 저자들은 manual design과 NAS 방식의 각각의 장점을 조합한 새로운 디자인 패러다임을 제시한다.

• manual desig와 같이 네트워크 구조를 설명이 가능하며 심플하고 모든 세팅을 아울러 잘 작동하는 네트워크를 만들 수 있는 general한 design principle을 발견하는 것을 목표로 한다.
• NAS와 같이 이러한 목표를 달성하도록 도와주는 semi-automated procedure의 장점을 활용한다.

결국, 전체적으로 하나의 특정 network instance를 만드는 것이 목표가 아닌 network의 population들을 파라미터화 시킨 design space를 디자인 하는 것이 목표이다.

Design space란?
앞서 manual과 NAS 같은 방식들은 비슷한 느낌으로 search space라는 말을 사용한다. 그러나 search space에서는 단 하나의 instance를 뽑아내는 게 목표였다면 여기서의 design space는 instance들을 뽑아내기 위한 스페이스를 직접 찾아내는 것이 목표이므로 design space라고 표현했다.

Tools for Design Space Design

Tool이라고해서 별건 없고 그냥 design space의 quality를 어떻게 quantify해서 평가를 하는지를 적어놨다.

단순히 search 방식 (manual or automated) 방식을 사용하거나 두 개의 design spaces로 부터 각각 찾아낸 best 모델들의 성능을 비교하는 것보다 distribution 자체를 비교하는게 더 robust하고 informative하다고 한다.

그렇기 때문에 모델의 distribution을 얻기 위해 design space에서 $n$개의 모델을 샘플링 후 학습을 진행한다.

이제 평가를 위한 tool은 error empirical distribution function (EDF)를 이용한다. 각각 error $e_i$를 가진 $n$개 모델로 측정한 error EDF는 아래와 같다.

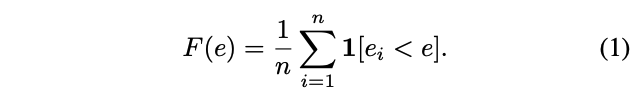
위 식은 다시 이해하자면 $\frac{error가 e_i보다 작은 모델의 수}{전체 모델의 수 (n)} $이다.

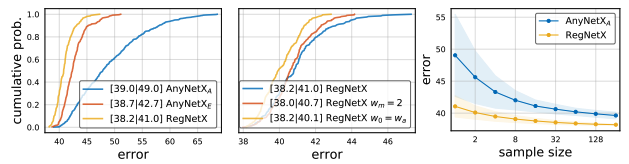
이제 이 식을 이용해서 아래의 가장 왼쪽 그래프를 그릴 수 있다. 뒤에서 설명하게 될 AnyNetX design space에서 500개의 샘플링된 모델을 사용하여 나타낸 것이다.

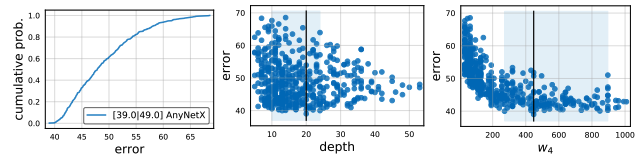
위 그림의 중간과 오른쪽은 다양한 네트워크의 property들을 나타낼 수 있다는 것을 보여주며 empirical bootstrap을 사용하여 측정할 수 있다.

The AnyNet Design Space

이제 AnyNet design space에 대해 설명할 차례다.

기본적인 구조는 아래와 같다.

네트워크의 기본 뼈대는 stem, body, head로 이루어져있고 이제 네트워크의 계산량과 성능에 영향을 크게 미치는 body 부분에 집중하여 수정을 진행하게 된다. 위 구조를 다시 애니메이션으로 나타내면 아래와 같다.

Body는 여러개의 stage로 이루어져있고 각 stage는 또 다시 여러개의 block으로 이루어져있다.

각 stage i 의 자유도는 block의 개수, width, 다른 block parameter들에 의해 결정된다. Block들은 stride에 따라 다르게 생기기도 했으며 아니면 아예 다른 종류의 block도 사용이 가능하다 (appendix 참고).

이제 AnyNetX는 16 degrees of freedom을 가지는데 이는 4개의 stage와 각 stage들은 다시 4개의 parameter들을 가지기 때문이다. 여기서 4개의 파라미터는 block의 개수 $d_i$, block width $w_i$, bottleneck ratio $b_i$, group width $g_i$를 의미한다. 쨋든 이 값들을 다 바꾸면서 생성가능한 design space가 AnyNetX의 것이며 굉장히 많은 조합으로 이루어져있다.

• 가능한 파라미터
  • $d_i \le 16$
  • $w_i \le 1024$ 중 8로 나누어떨어지는 수만 포함
  • $b_i \in \{1,2,4\}$
  • $g_i \in \{1,2,4,8,16,32\}$

이제 논문은 굉장히 자유로운 AnyNetX에서부터 조금씩 constraint를 붙여가며 RegNet까지 도달하는 방법을 보여준다. 이 과정을 그림으로 나타낸 것이 논문 1페이지에 떡하니 자리잡고 있는 figure 1.이다.

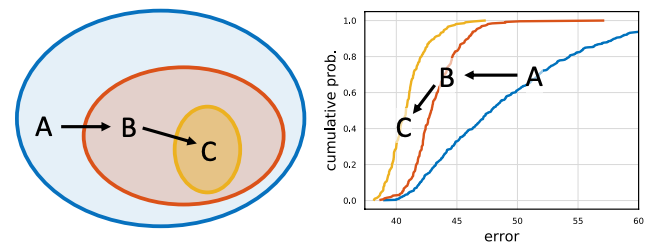
1. \(AnyNetX_A\)

방금 설명한 아무런 제약조건이 없는 AnyNetX를 의미한다. 굉장히 조합할 수 있는 경우의 수가 많으며 그러므로 자유도가 굉장히 높다.

2. \(AnyNetX_B\)

이제 \(AnyNetX_A\)에 bottleneck ratio에 대한 제약조건을 추가한다. 여기서 모든 스테이지에 대해 bottleneck ratio를 단 하나의 수로 고정을 시켜버린다 ($b_i = b$).

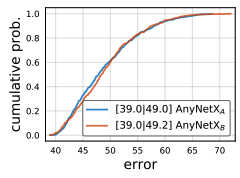
위 EDF 그림을 보면 하나로 고정했을 때와 아무런 제약조건이 없을 때가 차이가 없음을 볼 수 있다. 그래서 저자들은 그대로 고정시켜버린 후 진행을 계속한다.

3. \(AnyNetX_C\)

\(AnyNetX_B\)에 이번에는 shared group width를 사용하는 것이다. 즉, 모든 스테이지에 대해 group width도 하나의 같은 수로 고정해버린다 ($g_i = g$).

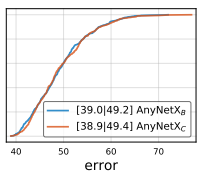
역시나 EDF의 큰 차이가 없음을 볼 수 있다.

이제 \(AnyNetX_C\)는 \(AnyNetX_A\)보다 자유도가 6 낮아졌다.

4. \(AnyNetX_D\)

이번에는 \(AnyNetX_C\)에 네트워크의 뒤로 갈수록 block의 width를 키우는 제약을 준다 ($w_{i+1} \ge w_i$).

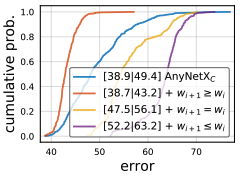
놀랍게도 이 제약을 줬을 때 성능이 더 좋아진 것을 볼 수 있다. (선이 그래프 왼쪽으로 치우칠수록 성능이 좋은 것!)

5. \(AnyNetX_E\)

\(AnyNetX_D\)에 비슷한 맥락으로 네트워크 뒤로 갈수록 block의 depth를 키우는 제약을 준다 ($d{i+1} \ge d_i$).

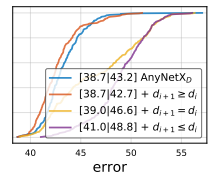
이 또한 성능을 개선할 수 있었으며 $w_i$와 $d_i$에 제약을 추가함으로써 디자인 스페이스가 $4!$ 만큼 줄어들었다.

이제 \(AnyNetX_E\)를 완성함으로써 design space가 줄어들었고 성능도 높여 더 좋은 모델을 뽑기가 좋아졌다.

AnyNetX에 대한 생성 과정은 아래의 동영상에 정리해뒀다.

The RegNet Design Space

이제 완성된 \(AnyNetX_E\)에서 더 깊은 insight를 얻기 위해 20개의 best 모델에 대한 성능을 그림으로 표현했다. 네트워크의 block 뒤로 갈수록 어떠한 width를 가지는지를 나타낸 것이다.

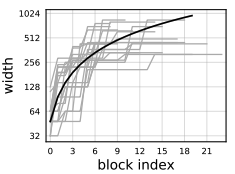
여기서 까만 선은 $0 \le j \le 20$에 대해 $w_j = 48·(j+1)$를 나타낸 것이며 log의 형태를 하고 있음을 살펴봐야한다.

위의 그래프에서 요즘 top model에서 많이 쓰이는 뒤로갈수록 width를 키우는 트렌드를 이해할 수 있게 되었다. 대신, log 선을 보면 각 block마다 다른 w를 사용하고 있지만 실제로는 어느 단계에 대해서는 같거나 큰 경우를 많이 채택하고 있다.

이제 좀 더 간결한 design space를 위해 선들을 quantize할 필요가 있다.

첫 번째로 block width에 대해 linear parameterization을 진행한다.

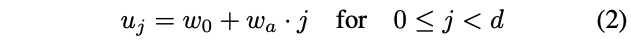
위 식은 3가지 parameter를 필요로 한다: depth $d$, initial width $w_0 > 0$, slope $w_a > 0$.

이제 다시 $u_j$를 quantize하기 위해 추가적인 parameter $w_m > 0$을 도입한다. 이는 width multiplier로 이전 stage의 width를 몇 배 할지 결정하는 파라미터이다.

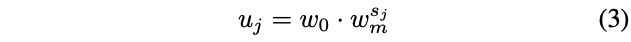
위 식으로 각 block j에 대한 $s_j$를 계산하면 된다.

그리고 난 뒤 $u_j$를 quantize하는데 앞서 구한 $s_j$에 round를 취한 뒤 quantize된 per-block width인 $w_j$를 구할 수 있다.

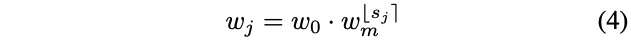
이제 constant width를 가진 블록들의 수를 세서 per-block width $w_j$를 per-stage 폼으로 나타낼 수 있게 되었다.

즉, 각각의 stage i에서 block width는 $w_i = w_0·w_m^i$로 나타낼 수 있고 block의 수는 아래와 같이 나타낼 수 있다.

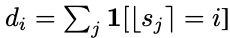
조금 복잡하기는 한데 그냥 간단히 모델을 생성하는 design space를 공식을 통해서 쉽게 구할 수 있게 되었다고 생각하면 된다.

결국 네트워크의 구조는 6개의 파라미터: $d, w_0, w_a, w_m, b, g$로 결정이되며 이러한 design space를 regular network, 줄여서 RegNet이라고 부르기로 한다. 여기서 RegNet은 RegNetX와 같으며 RegNetX 모델에 SE (Squeeze-and-Excitation) 연산을 추가한 것을 RegNetY라고 부르기로 한다. RegNetX의 성능은 아래와 같다.

Analyzing the RegNetX Design Space

RegNet trends.

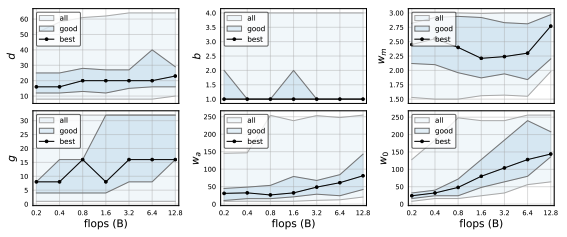
RegNetX의 trend는 위 그림에서 볼 수 있다. 베스트 모데의 depth는 모든 regime에 대해서도 안정적으로 비슷한 값을 가지고 있고 최적의 depth는 ~20 block 정도이다. 이는 더 높은 flop 을 위해 더 딥한 모델을 사용하는 현실과 대조적인 결과이다.

베스트 모델에 대한 bottleneck ratio b 는 1.0이라 bottleneck 없이 하는 것이 가장 최적의 성능을 보이고 있었다.

Width multiplier $w_m$는 2.5정도로 최근 모델들은 2배를 하고 있는 것과 비슷한 양상을 보이고 있다.

Complexity analysis.

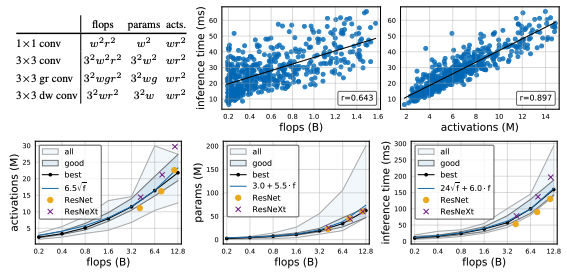
Conv layer의 output의 크기를 뜻하는 activation은 자주 측정되는 값은 아니지만 runtime에 큰 영향을 미치는 요인 중 하나이다. RegNet에서 베스트 모델들은 이 activation이 square-root로 flop에 따라 증가하고 있고 파라미터들은 linear하게 증가하는 것을 위 그림에서 볼 수 있다.

RegNetX constrained.

저자들은 RegNetX의 design space를 다음과 같이 정의한다.

• $b = 1$, $d \le 40$, $w_m \ge 2$
• parameter와 activation에 제한을 둔다. –> square-root와 linear하게 증가하도록.

이렇게 제한을 두면서 재정의한 RegNetX design space의 결과는 아래 그림에서 볼 수 있다.

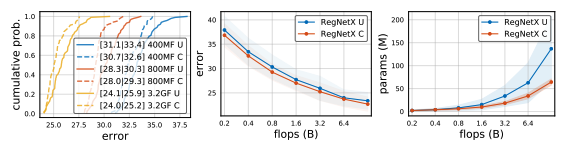
Comparison to Existing Networks

앞서 잠깐 언급한 SE 연산을 추가한 모델은 RegNetY를 여기서 다시 볼 수 있다.

재정의한 RegNetX와 RegNetY에서 각각 25개의 무작위 세팅에서 뽑은 베스트 모델을 선별하고 이 베스트 모델을 5번 100에폭씩 돌린 결과를 아래의 그림에서 볼 수 있다.

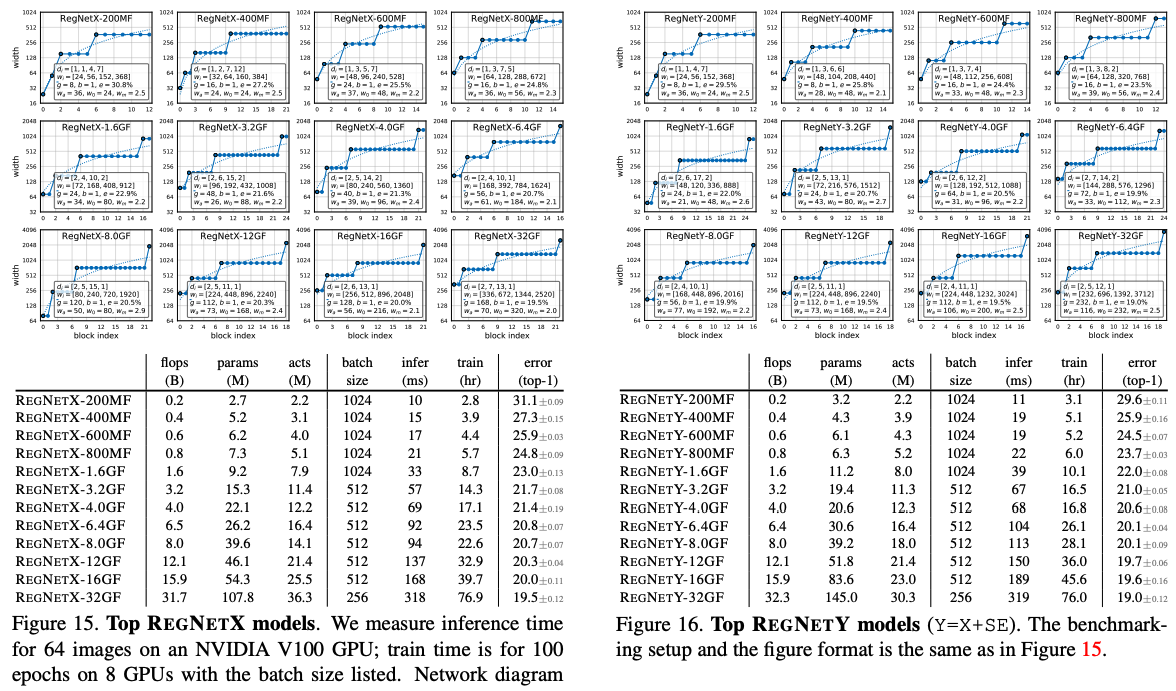
대략적으로 기억해야 할 포인트는 더 높은 flop을 가진 모델일 수록 3번째 스테이지에서 block의 개수가 제일 많았고 마지막 스테이지에서는 굉장히 적은 수의 block을 가지는 것을 볼 수 있다. 또한 group width g는 더 큰 모델에 따라 그 값이 증가했고 depth d는 saturation되는 볼 수 있다.

Mobile Regime

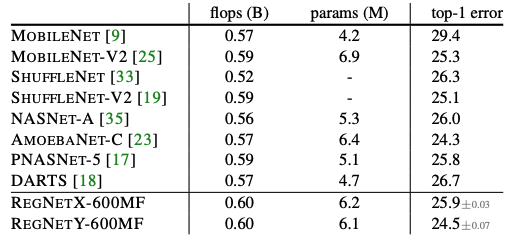
모바일에 들어가야하는 모델들은 그 크기가 작지만 성능은 좋아야한다. 위의 표에서 볼 수 있듯이 RegNet은 성능이 좋았고 심지어 이 결과는 아무것도 추가하지 않은 basic한 모델이므로 더욱 성능이 좋아질 수 있다. 따로 아메바넷에 대해 읽어보지는 않았지만 성능이 좀 많이 좋아서 놀라긴했다.

Full Regime

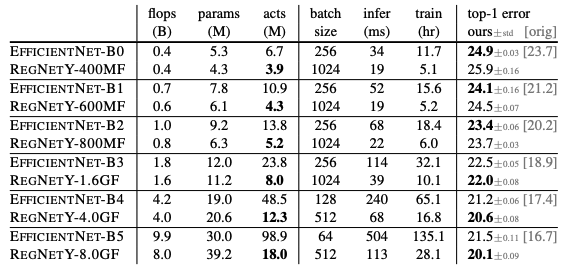
전체적인 비교는 최근까지 SOTA 성능을 보이는 Google의 EfficientNet과 비교를 했다. Network 구조 자체의 성능만을 철저히 비교하기 위해서 EfficientNet을 저자들이 직접 다시 구현했다고 한다.

낮은 flop에서는 EfficientNet이 성능이 더 좋았고 높아질수록 RegNetY와 RegNetX 모두 EfficientNet보다 좋아짐을 볼 수 있다. 또한 EfficientNet의 경우, activation이 flop에 따라 linear하게 증가하고 RegNet은 square-root 로 증가하기 때문에 GPU에서의 속도차이가 난다. 그 결과 RegNet은 EfficientNet보다 5배 정도 빠르고 더 적은 에러를 달성하였다.

Summary

1. 다양한 환경에서 잘 작동할 수 있는 모델을 만들기 위해 design space를 디자인한다.
2. Design space의 quantized linear function을 통해 더욱 simple하게 space를 정의할 수 있게 되었다.
3. 네트워크 구조를 잘 이해할 수 있게 되었고 EfficientNet 모델보다 GPU에서 속도가 5배 빠름을 증명하였다.

다 읽고…

최근까지 계속해서 EfficientNet을 많이 쓰고 있던터라 이런 더 좋은 모델이 나왔다는 것을 늦게 깨닫게 되었다. 물론 이 모델조차도 supervised learning에 맞춰 나온 것이겠지만 self-supervised learning에도 좋은 결과를 보일 수 있을 거라 생각한다. 공식을 통해 design space를 정의하는 것이 굉장히 깔끔하게 누구나 사용하기 쉽게 되어있다는 느낌을 많이 받았고 Facebook에서 github에 오픈 소스로 공개해주었으니 다음 프로젝트에는 RegNet 모델을 사용해봐야겠다.

—— 추후 작성 ——