A Comprehensive Overhaul of Feature Distillation

Byeongho Heo, Jeesoo Kim, Sangdoo Yun, Hyojin Park, Nojun Kwak, Jin Young Choi
[Naver]
Submitted on 3 Apr 2019 (v1), last revised 9 Aug 2019 (this version, v2)
arXiv:1904.01866

지난 주 열렸던 KCCV 학회에서 포스터 세션에서 알게된 논문이다. 생각보다 나온지 조금 지난 논문이길래 놀랐다.

Knowledge distillation만 알았는데 feature distillation이라는 것은 이 논문으로 사실상 처음 접했다. 끝단의 output에서만 feature가 같아지도록 하는 것이 아닌 layer block 사이에서의 feature 도 teacher(이후 T)와 student(이후 S)가 서로 같아져야 하는 것이 핵심 부분이다.

Intro

Network compression (model을 더 작게, cost-efficient하게 만드는 기술)

• model pruning
• model quantization
• knowledge distillation

여기서 knowledge distillation은 위의 2개와는 다르게 T와 S의 구조적 차이에 관계없이 네트워크를 downsize할 수 있다. 이러한 이유때문에 KD는 network compression에 차세대 접근법이 되었다. 근데 사실 엄청난 성능을 보여주는 teacher network의 output은 결국 ground truth와 크게 다를바 없어진다. 즉, 그냥 S를 GT를 가지고 학습하는 것과 다를 바가 없다는 것이다. GT와 다르게 T만이 학습한 더 유익한 정보들을 더 잘 활용하고 싶어서 나온 것이 “feature distillation”이다.

지금까지 나온 feature distillation들은 KD보다 성능을 높일 수 있었지만 본 논문 저자들은 T의 feature value를 변형시켜 더 개선될 여지가 남아있다고 주장한다. 그래서 저자들은 새로운 feature distillation loss를 제안하는 데 이는 아래 4가지 측면에서 고려된 방식이다.

• teacher transform
• student transform
• distillation feature position
• distance function

Motivation

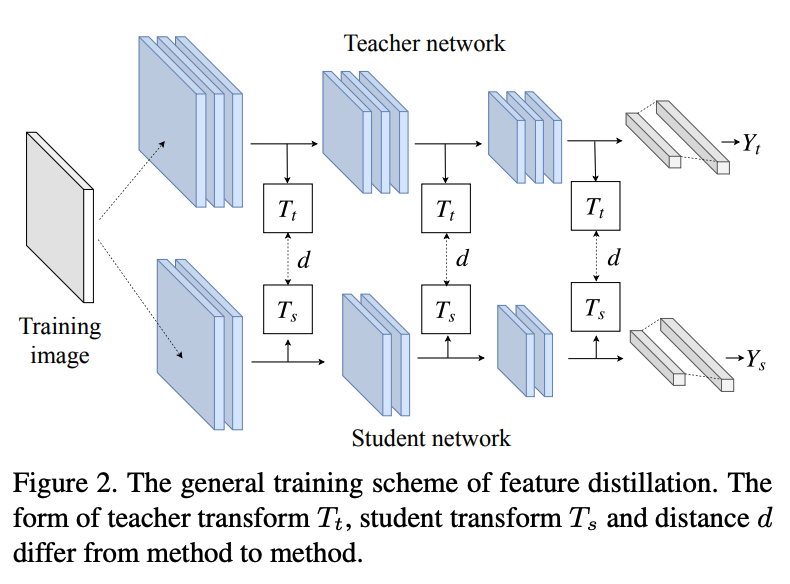
T의 feature는 \(F_t\)
S의 feature는 \(S_t\)

이 둘의 차원을 맞추기 위해서 각각 \(T_t\), \(T_s\) 를 통해 변환시킨다.

feature distillation의 loss function을 일반화시키면 아래와 같다.

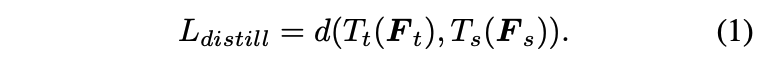
S는 이 \(L_{distill}\)을 최소화하는 방향으로 학습을 시킨다.

이 \(L_{distill}\)은 T에서 학습한 모든 중요한 정보가 잃어버림없이 전달되도록 하는 것이 이상적이다. 이제 이 \(L_{distill}\)를 디자인하기 위해서 4가지 측면을 살펴본다.

Teacher transform

Teacher transform \(T_t\)는 distillation 에서 information missing의 주요 원인이 된다.

FitNets을 제외한 대부분의 teacher transforms들(AT, FSP, Jacobian, FT, AB)은 information loss를 일으킨다.

• AT, FSP, Jacobian : \(T_t\)로 feature vector의 차원을 줄임 –> 심각한 정보 손실 발생.
• FT : 유저가 직접 결정하는 compression ratio를 사용 –> original과 달라져서 정보 손실 발생.
• AB : original feature를 binarized values의 형태로 사용. –> original과 달라져서 정보 손실 발생.

중요한 것은 feature에는 도움이 되는 info와 그렇지 않은 info가 존재하는데 이 때 도움이 되는 info를 잃어버리지 않도록 해야 한다.

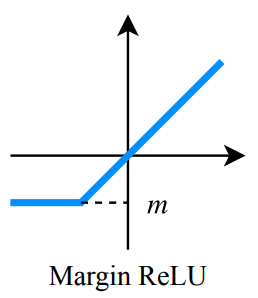
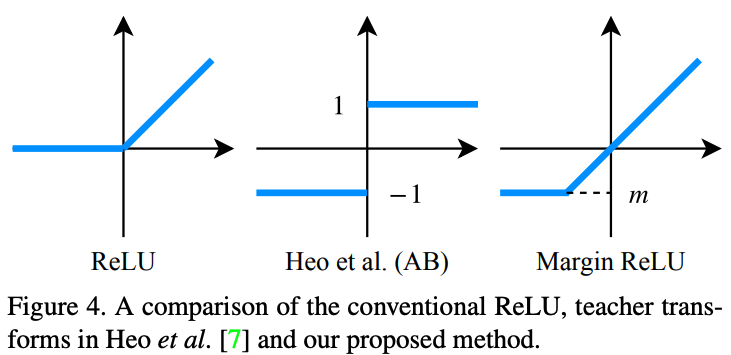
그래서 이 논문에서는 teacher transform을 위해 margin ReLU라는 새로운 ReLU activation을 제안한다. Margin ReLU를 사용하면 positive(beneficial) 정보는 아무런 변형없이 그대로 살아있게 되고 반대로 negative(adverse) 정보는 압축이 된다.

Student transform

전형적으로 \(T_s\)는 \(T_t\)와 동일한 function을 사용한다. 때문에 이러한 방식을 사용하는 AT, FSP, Jacobian, FT에서는 \(T_s\), \(T_t\) 모두에서 동일한 양의 정보 손실이 발생한다.

FitNets와 AB는 \(F_t\)의 차원을 줄이지 않고 이 차원과 \(F_s\)의 차원을 맞추기 위해 \(T_s\)로 1×1 conv를 사용한다. 이 경우, \(F_s\)의 사이즈가 커지기 때문에 정보 손실이 없다.

때문에 본 논문에서도 동일한 방식으로 1×1 conv layer를 사용한다.

Distillation feature position

FitNets과 같이 임의의 중간 layer의 끝에서 distillation하는 것은 오히려 좋지않은 성능을 보인다.

Wide residual networks, Deep pyramidal residual networks에서 동일한 방식으로 layer들을 grouping한다.

• AT, FSP, Jacobian : 각 그룹의 끝에서 distill.
• FT : 오직 마지막 layer 그룹에서 distill.

위 두 위치는 FitNets보다는 좋은데 ReLU를 고려하지 않은 위치이다. ReLU는 positive만 패스하고 negative는 거르는데 이러한 information dissolution을 좀 더 이해하고 distillation position을 정해야한다는 것이다.

즉, pos와 neg를 포함한 모든 정보가 전달될 수 있도록 ReLU 앞에서 distillation을 진행해야 한다. 이 위치를 pre-ReLU라고 칭한다.

Distance function

대부분의 방식들은 naive하게 L2나 L1 distance를 사용한다. 대신, 저자들은 \(T_t\)와 pre-ReLU에 알맞은 새로운 distance function(partial L2 distance)을 제안한다.

사실 pre-ReLU를 사용하면 adverse info도 포함하게 된다. 그렇기 때문에 이 neg 정보들을 전달하지 않도록 하는 partial L2 distance를 사용한다.

Approach

Distillation position

activation function은 neural network에서 중대한 구성요소이다. ReLU의 경우 앞서 말했듯이 negative value들을 0으로 만든다. 이를 통해 불필요한 정보들이 backward로 가지 못하게 막을 수 있다. 이러한 특성을 잘 활용하면 오직 필요한 정보만 전달할 수 있지 않을까?

이전의 distillation 기법들은 activation function에 대한 깊은 고려를 하지 않았다. 대신, 저자들은 distillation의 위치를 layer block의 끝과 다음에 이어지는 첫번째 ReLU 사이로 정했다.

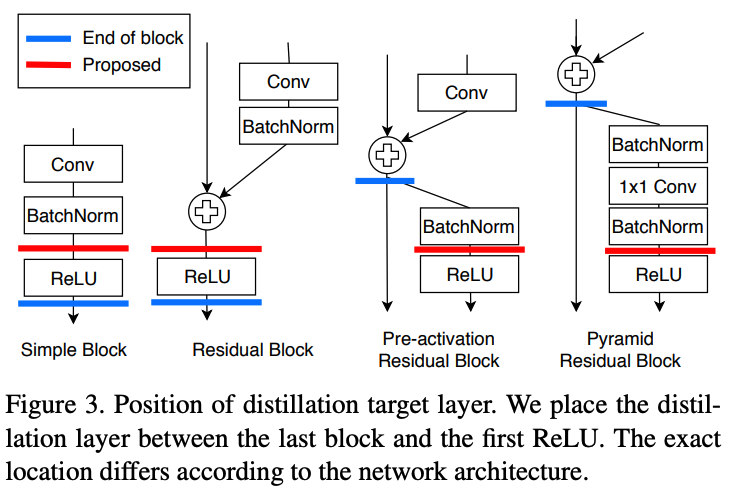
이러한 위치는 ReLU를 지나기 전 teacher의 정보들을 student가 얻을 수 있게 한다. 특별한 distillation 위치 덕분에 저자들은 student의 성능을 매우 높일 수 있었다고 한다.

Loss function

teacher의 feature value인 \(F_t\)는 방금 위에서 ReLU 이전의 값들을 사용한다고 했다. positive value는 teacher에 의해 활용되는 정보를 가지고 있는 반면, negative value들은 버려진다.

여기서 student는 teacher의 뉴런과 동일한 activation status를 생성해야한다. 즉, teacher의 값이 pos면 student도 같은 value를 생성해야만 하며 teacher의 값이 neg면 stu는 0보다 작은 값을 만들어야한다.

Knowledge transfer via distillation of activation boundaries formed by hidden neurons.라는 논문에서 student의 값이 0보다 작게 만들기 위해서는 margin이 필요하다고 한다. 그래서 본 논문에서는 pos는 유지하되 neg에는 margin을 줘서 0보다 작은 값을 만들어내도록 하는 teacher transform을 사용한다.

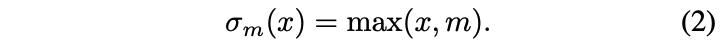
\(m\)은 0보다 작은 margin 값이다.

Knowledge transfer via distillation of activation boundaries formed by hidden neurons.에서는 margin 값을 임의의 스칼라 값으로 설정했지만 저자들은 채널별 negtaive response의 기대값으로 설정했다. 즉, margin ReLU는 input의 각 채널에 대응되는 값들을 사용하게 된다 (채널별로 달라짐).

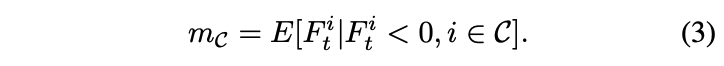
Expectation value는 training 과정에서 바로 계산이 가능하며 또는 이전 BN layer의 parameter로도 계산이 가능하다.

student transform으로는 1×1 conv layer와 batch normalization layer로 구성했다.

Distance function \(D\)를 보자. \(D\)는 ReLU를 고려하는 방향으로 바껴야한다. teacher의 feature값이 pos이면 그대로 전달되어야 하지만 neg의 경우는 다르다. 만약 student의 값이 target보다 크면 그 값은 줄어들어야 하며 더 작은 경우 증가시킬 필요는 없다. 어차피 ReLU에 의해서 negative 값들은 걸러지기 때문이다.

따라서 partial \(L_2\) distance function \(d_p\)는 다음과 같이 정의된다.

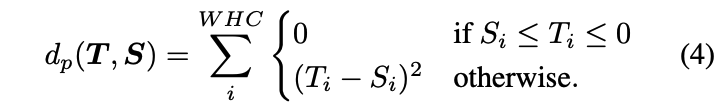
이제 위의 식들을 모두 종합하여 distillation loss를 정의해보자. teacher transform \(T_t\)로는 marin ReLU \(\sigma{m_c}(x)\)를 사용하고 1×1 conv로 구성된 student transform \(T_s\)는 regressor \(r(·)\)으로 표시한다.

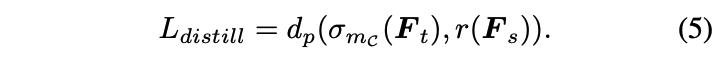
Final loss는 distillation loss와 task loss의 합으로 표시한다.

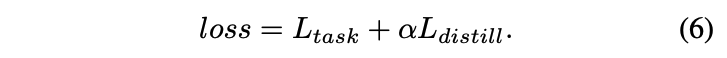
Batch Normalization

BN은 최근 network architecture에서 학습을 안정화시키기 위해서 사용된다. BN에는 training mode와 evaluation mode가 존재하는데 전형적으로 student의 feature 은 normalized batch이기 때문에 teacher의 것도 normalize되어야 한다.

즉, teacher의 BN layer는 distillation 때 training mode가 되어야하고 student transform에서 1×1 conv 뒤에 BN layer를 추가해야한다.

이러한 BN 방식을 사용하면 성능이 더 올라간다.

다 읽고..

실험 부분은 건너뛴다…ㅎ proposed 방식이 최고 성능을 보였다는 내용은 모든 논문이 동일하므로..

feature distillation 관련 논문은 처음 읽어보는 것이라 다른 방식들에 대한 사전지식이 없어 조금 서로를 비교하는 게 힘들었다. 그래도 이러한 기법이 있다는 것을 알게된 좋은 기회였다.