Large Batch Training of Convolutional Networks (LARS)

Yang You, Igor Gitman, Boris Ginsburg
(Submitted on 13 Aug 2017 (v1), last revised 13 Sep 2017 (this version, v3))
arXiv:1708.03888

NVIDIA에서 2017년에 내놓은 논문이다. 큰 배치 사이즈와 큰 learning rate를 이용하여 accuracy를 떨어트리지 않고도 빠르게 학습할 수 있는 방법을 제시했다.

큰 CNN을 학습시키는 건 시간이 많이 걸린다. 이 시간을 단축하는 brute-force 방식이 GPU와 같은 computational unit을 추가하고 data-parallel SGD를 사용하여 네트워크를 학습시키는 것이다. 이 때 unit 각각의 worker들은 글로벌 미니배치의 chunk(일부분)을 받아 일하게 되는데 이 chunk의 크기는 worker들의 계산 리소스를 충분히 활용할 수 있을 정도로 커야한다. 즉, worker의 수를 늘리는 것은 배치 사이즈의 증가를 야기한다.

흔히 Stochastic Gradient (SG) 기반 방식을 사용하여 CNN을 학습한다. Step \(t\)에서 각 미니배치 샘플 \(x_i\)에 대해서 gradients of loss function \(\nabla L(x_i, w)\)을 계산하고 이 stochastic gradient를 기반으로 네트워크 weight \(w\)를 업데이트한다.

이 때 SG은 \(N\)개의 unit에 의해 병렬적으로 계산될 수 있는데 각각의 unit들은 \(\cfrac{B}{N}\)개의 샘플로 이뤄진 chunk를 계산한다.

Linear LR Scaling

2014년도 Google의 Krizhevsky가 큰 배치를 사용하기 위해서는 LR 또한 늘려줘야한다고 주장했다. 즉, 배치사이즈를 \(k\)배하면 LR 또한 \(k\)배하고 그 이외의 모든 하이퍼 파라미터들은 그대로 둬야한다고 했다. Linear LR scaling의 로직은 간단하다. 총 이미지가 300개가 있을 때 기존 미니배치 사이즈가 10인 경우 총 step은 30번을 돌아야한다. 미니배치 사이즈를 30으로 늘렸을 때 (×3) 총 step은 10번으로 줄어든다 (×\(\frac{1}{3}\)).

식으로 보자. \(k=2\)인 경우이다. 배치사이즈가 B일 때, 2번의 반복 후 weight update는 다음과 같다.

그리고 LR가 \(\lambda_2\)이고 배치사이즈를 2배로 늘렸을 때는 다음과 같다.

(2)식에서 \(\nabla L(x_j, w_{t+1}) \approx L(x_j, w_t)\)라고 가정했을 때, \(\lambda_2 = 2×\lambda\) 를 대입하면 두 식은 거의 동일한 값을 가지게 된다.

이 방식은 Alexnet에서 배치사이즈 2K이상에서는 학습이 잘 안된다고 한다. 너무 큰 LR이 수렴하지 못하고 발산했기 때문이다. Codreanu et al.에 따르면 이 linear scaling은 Batch Normalization을 사용하는 네트워크에서 더욱 효과를 발휘한다고 한다.

LR warm-up

배치를 늘려가는 것에 있어서 가장 큰 문제는 큰 LR로 인해 발생하는 불안정함 때문이다. 학습 초기에 너무 큰 LR로 인해 발생하는 불안정함을 극복하기 위해서 Facebook [Goyal et al.]에서 한 가지 방법을 제안했다. 학습 초기에 아주 작은 LR로 학습을 시작하고 이를 점진적으로 키워나가는 LR warm-up 방식을 선보였다. Warm-up 기간이 끝나면 (대부분 아주 적은 수의 에포크) 그냥 다시 polynomial decay와 같은 보통의 LR policy로 바꿔서 학습을 진행하면 된다. LR warm-up과 linear scaling을 Resnet-50에 같이 사용했을 때 배치 \(B=8K\)일 때까지 baseline과 크게 점수차가 나지 않았다. (손상 거의 없음)

Generalization Gap

큰 배치 학습의 또 다른 문제는 Keskar et al.에서 제시한 generalization gap이다. 이들은 배치가 커질 수록 generalization 능력이 떨어지는데 이 때 원인이 큰 배치를 사용하면 training function에서 **sharp minima”로 빠질 위험이 크기 때문이라고 설명했다.

위의 그림에서 폭이 좁은 곳이 sharp minima이다. Flat에 비해 굉장히 폭이 좁은 것을 볼 수 있다. 이 때 얘가 왜 문제가 되느냐 하면 밑의 그림을 보면 이해가 될 것이다.

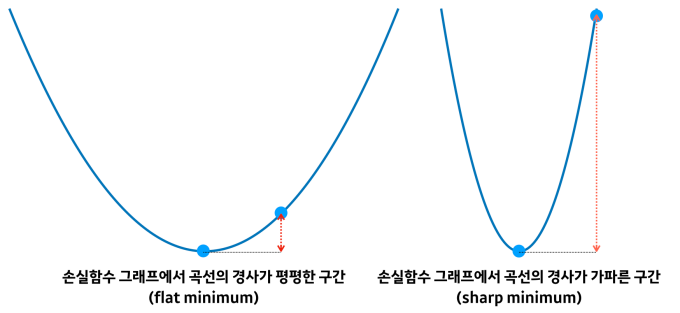출처 : https://www.kakaobrain.com/blog/113

왼쪽과 오른쪽 그래프에서 동일한 크기 만큼 옆으로 옮겨갔을 때 오른쪽 그래프에 비해 왼쪽 가파른 그래프에서는 로스가 굉장히 커지는 것을 볼 수 있다. 이렇게 되면 테스트 시 오차가 입력 데이터에 따라 매우 큰 폭으로 변할 수 있어 generalization 능력이 떨어진다는 것이다.

LARS 적용에 앞서 저자들은 큰 배치를 사용한 Alexnet을 학습시켜보았다. 베이스라인으로 B=512인 경우를 사용했고 SGD에 모멘텀은 0.9, 초기 LR은 0.01 후에 polynomial (power=2) decay LR policy를 적용했다. 총 에폭은 100을 학습시켰다. BN이 없는 왼쪽 표 버전은 warm-up도 적용했고 오른쪽의 BN의 경우 warm-up없이도 큰 LR을 적용할 수 있었다.

–> [여담] :) polynomial decay policy는 코드를 보면 대충 이해가 간다.

Table 1: Alexnet and Alexnet-BN: B=4K and 8K.

BN을 적용했을 때 더 큰 learning rate를 사용할 수 있었다. 오른쪽 표인 BN을 사용한 alexnet에서 배치가 8K일 때 accuracy(58.0%)는 여전히 베이스라인의 것(60.2%)보다 2.2%가 낮았다. 이 갭이 과연 앞서 말한 generalization gap인지 확인하기 위해 train/test 사이의 차이를 그래프로 나타내보았다.

Figure 1: Alexnet-BN: Gap between training and testing loss

이들은 그래프를 보고 generalization gap과 관련이 없는 accuracy loss라고 단정지었다.

Layer-Wise Adaptive Rate Scaling (LARS)

표준 SGD는 모든 layer에 대해 다 동일한 LR을 사용한다: \(w_{t+1} = w_t - \lambda \nabla L(w_t)\). 이 때 이 식에서 \(\lambda\)가 너무 커져버리면 \(\vert \vert \lambda * \nabla L(w_t) \vert \vert\)가 \(\vert \vert w \vert \vert\)보다 커지게 되고 결국 divergence의 원인이 된다. 이게 바로 학습 초기에 weight initialization 과 initial LR에 민감한 이유이다.

이들은 서로 다른 층에서 weights와 biases에 따라 weight&gradient의 L2-norm 비율(\(\frac{\vert \vert w \vert \vert}{\vert \vert \nabla L(w_t) \vert \vert}\))이 굉장이 달라진다는 것을 발견했다. 한번의 iteration gndml AlexNet-Bn을 살펴보자.

Table 2: AlexNet-BN: The norm of weights and gradients at 1st iteration.

위의 표에서 FC6에서의 비율이 1345로 매우 큰 것을 볼 수 있다. 그리고 이 비율들은 에포크를 돌면 돌 수록 감소하는 것을 Figure 2. 에서 볼 수 있다.

Figure 2: LARS: local LR for different layers and batch sizes

이들은 unstable함을 없애기 위해서 새로운 접근을 사용했다. 각각의 layer \(l\)에 대한 local LR \(\lambda^l\)를 사용했다.

여기서 \(\gamma\)는 global LR이다. Local LR \(\lambda^l\)은 “trust” 계수를 통해 각각의 layer에 대해 정의된다:

그리고 이는 SGD로 확장하기 위해 local LR와 weight decay term \(\beta\)의 밸런스를 맞추도록 다시 정의 된다:

LARS를 적용한 SGD network 학습은 Algorithm 1에 요약된다.

Training with LARS

[AlexNet]

LARS를 사용하면 AlexNet과 AlexNet-BN을 32K까지 배치를 올릴 수 있었다. Figure 3.을 보면 8K를 사용한 두 모델 모두 베이스라인의 성능을 어느정도 따라잡았다.

Figure 3: LARS: Alexnet-BN with B=8K

Table 3. 를 보면 베이스라인 B=512일 때와 비교하여 AlexNet-BN이 B=16K일 때는 0.9% 낮았고 32K일 때는 2.6% 낮았다.

Table 3: Alexnet and Alexnet-BN: Training with LARS

[ResNet-50]

베이스라인은 B=256, top-1 accuracy가 73%일 때로 잡았다. 모든 네트워크는 SGD(momentum 0.9), weight decay=0.0001이고 90에포크 동안 학습됐다. LARS를 적용했고 5에포크 동안 warm-up도 사용했다.

Table 4: ResNet50 with LARS.

결과적으로 배치는 32K까지 올릴 수 있었고 성능도 베이스라인과 거의 비슷했다. (-0.7%)

다 읽고..

며칠씩이나 걸리는 네트워크 학습에 있어서 빠르게 학습시키는 방법에 대해 누구나 갈증을 느끼고 있을 것이다. 큰 배치와 큰 LR을 이용하여 빠르게 학습할 수 있도록 한 점은 높이 살만하지만 생각보다는 성능의 차이가 아주 작게라도 존재하는 것을 보고 실망을 전혀 안했다고는 못하겠다..ㅎ 그래도 엄청 좋은 방법임은 틀림없다.

아 또한 이 논문은 LARS를 SGD 전용으로 내놨었는데 이를 카카오브레인에서 SGD와 분리시켜 어느 optimizer에도 LARS를 적용시킬 수 있도록 개발했다. 해당 소스 코드는 https://github.com/kakaobrain/torchlars 여기에서 볼 수 있다.